
分析 (1)由f(-x)=$\frac{{e}^{-x}-1}{{e}^{-x}+1}$=$\frac{1-{e}^{x}}{1+{e}^{x}}$=-f(x),可知f(x)=$\frac{{e}^{x}-1}{{e}^{x}+1}$为奇函数,g(x)+g(2-x)=f(x-1)+f(1-x)+2,即g(x)+g(2-x)=2,由an=g($\frac{1}{n}$)+g($\frac{2}{n}$)+g($\frac{3}{n}$)+…+g($\frac{2n-1}{n}$),采用倒叙相加法,即可求得数列{an}的通项公式;
(2)bn=$\frac{2{S}_{n}-n}{n+c}$,则b1=$\frac{1}{1+c}$,b2=$\frac{6}{2+c}$,b3=$\frac{15}{3+c}$,由等差数列的性质2b2=b1+b3,即可求得常数c;
(3)由(1)可知cn=$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),采用“裂项法”即可求得Tn=$\frac{n}{2n+1}$,由$\frac{k}{57}$<(Tn)min=$\frac{1}{3}$,即可求得k的取值范围,求得对一切n∈N*都成立的最大正整数k的值.
解答 解:(1)由f(-x)=$\frac{{e}^{-x}-1}{{e}^{-x}+1}$=$\frac{1-{e}^{x}}{1+{e}^{x}}$=-f(x),
函数f(x)=$\frac{{e}^{x}-1}{{e}^{x}+1}$为奇函数,
g(x)+g(2-x)=f(x-1)+1+f(2-x+1)+1=f(x-1)+f(1-x)+2,
由f(x)=$\frac{{e}^{x}-1}{{e}^{x}+1}$为奇函数,
f(x-1)+f(1-x)=0
∴g(x)+g(2-x)=2,
∵an=g($\frac{1}{n}$)+g($\frac{2}{n}$)+g($\frac{3}{n}$)+…+g($\frac{2n-1}{n}$),n∈N*,①
an=g($\frac{2n-1}{n}$)+g($\frac{2n-2}{n}$)+g($\frac{2n-3}{n}$)+…+g($\frac{1}{n}$),n∈N*,②
①+②得2an=[g($\frac{1}{n}$)+g($\frac{2n-1}{n}$)]+[g($\frac{2}{n}$)+g($\frac{2n-2}{n}$)]+…+[g($\frac{2n-1}{n}$)+g($\frac{1}{n}$)]=$\underset{\underbrace{2n-1}}{2+2+2+…+2}$=2(2n-1),
∴an=2n-1;
(2)bn=$\frac{2{S}_{n}-n}{n+c}$,则b1=$\frac{1}{1+c}$,b2=$\frac{6}{2+c}$,b3=$\frac{15}{3+c}$,
由题意得:2b2=b1+b3,
∴c=-$\frac{1}{2}$;
(3)cn=$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
∴数列{cn}的前n项和为Tn,Tn=c1+c2+…+cn,
=$\frac{1}{2}$[(1-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{5}$)+…+($\frac{1}{2n-1}$-$\frac{1}{2n+1}$)],
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$),
=$\frac{n}{2n+1}$,
∴$\frac{n}{2n+1}$>$\frac{k}{57}$,对一切n∈N*都成立
∴$\frac{k}{57}$<(Tn)min=$\frac{1}{3}$,则k<19,
∴kmax=18,
使不等式Tn$>\frac{k}{57}$对一切n∈N*都成立的最大正整数k的值18.
点评 本题考查等差数列的通项公式及前n项和公式,考查函数的奇偶性,考查利用“错位相减法”,“倒叙相加法”求数列的前n项和及通项公式,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0或2$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 0或-2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {(1,2)} | C. | {(2,1)} | D. | {(x,y)|x=1或y=2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
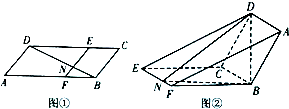 如图①,已知ABCD为平行四边形,∠A=60°,AF=2FB,AB=6,点E在CD上,EF∥BC,BD⊥AD,BD交EF于点N,现将四边形ADEF沿EF折起,使点D在平面BCEF上的射影恰在直线BC上(如图②),则折后直线DN与直线BF所成角的余弦值为$\frac{{\sqrt{3}}}{4}$.
如图①,已知ABCD为平行四边形,∠A=60°,AF=2FB,AB=6,点E在CD上,EF∥BC,BD⊥AD,BD交EF于点N,现将四边形ADEF沿EF折起,使点D在平面BCEF上的射影恰在直线BC上(如图②),则折后直线DN与直线BF所成角的余弦值为$\frac{{\sqrt{3}}}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com