
已知函数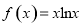 ,
, 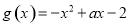 .
.
(1)求函数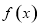 在
在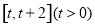 的最小值;
的最小值;
(2)若函数 与
与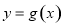 的图象恰有一个公共点,求实数
的图象恰有一个公共点,求实数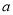 的值;
的值;
(3)若函数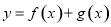 有两个不同的极值点
有两个不同的极值点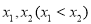 ,且
,且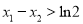 ,求实数
,求实数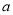 的取值范围.
的取值范围.
科目:高中数学 来源:2015-2016学年贵州黔南州高一下学期期末数学试卷(解析版) 题型:解答题
已知数列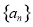 的前n项和Sn满足
的前n项和Sn满足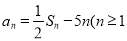 且
且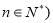
(I)求证:数列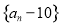 为等比数列
为等比数列
(II)记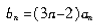 ,求数列
,求数列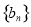 的前n项和Tn
的前n项和Tn
查看答案和解析>>
科目:高中数学 来源:2016届陕西黄陵中学高三下二模考试数学(理)试卷(解析版) 题型:填空题
已知双曲线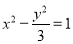 的左右焦点分别为
的左右焦点分别为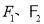 ,
,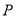 为双曲线右支上一点,点
为双曲线右支上一点,点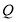 的坐标为
的坐标为 ,则
,则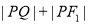 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目:高中数学 来源:2016届陕西黄陵中学高三下二模考试数学(理)试卷(解析版) 题型:选择题
设等比数列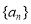 的前
的前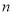 项和为
项和为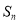 ,若
,若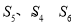 成等差数列,则数列
成等差数列,则数列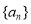 的公比
的公比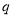 的值等于( )
的值等于( )
A.-2或1 B.-1或2 C.-2 D.1
查看答案和解析>>
科目:高中数学 来源:2017届甘肃武威二中高三上学期月考二数学(文)试卷(解析版) 题型:解答题
某企业接到生产3000台某产品的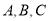 三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产
三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产 部件6件,或
部件6件,或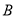 部件3件,或
部件3件,或 部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产
部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产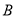 部件的人数与生产
部件的人数与生产 部件的人数成正比,比例系数为
部件的人数成正比,比例系数为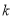 (
( 为正整数).
为正整数).
(1)设生产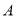 部件的人数为
部件的人数为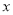 ,分别写出完成
,分别写出完成 三件部件生产需要的时间;
三件部件生产需要的时间;
(2)假设这三种部件的生产同时开工,若 ,求完成订单任务的最短时间,并给出此时具体的人数分组方案.
,求完成订单任务的最短时间,并给出此时具体的人数分组方案.
查看答案和解析>>
科目:高中数学 来源:2016届浙江稽阳联谊学校高三4月联考数学(理)试卷(解析版) 题型:解答题
已知数列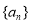 满足:
满足: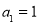 ,
,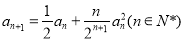 .
.
(1)求最小的正实数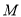 ,使得对任意的
,使得对任意的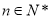 ,恒有
,恒有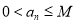 ;
;
(2)求证:对任意的正整数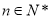 ,恒有
,恒有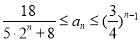 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com