
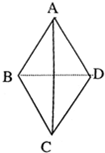
 设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.| 1 |
| 2 |
| 3 |
| 6 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
| 5 |
| 36 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 3 |


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年孝感高中高一下学期期末考试数学卷 题型:解答题
(本小题满分12分)
 设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
求:(Ⅰ)投了2次骰子,棋子才到达顶点B的概率;
(Ⅱ)记投了n次骰子,棋子在顶点B的概率为 .求
.求 .
.
查看答案和解析>>
科目:高中数学 来源:2010年孝感高中高一下学期期末考试数学卷 题型:解答题
(本小题满分12分)
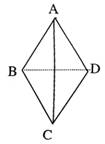 设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
求:(Ⅰ)投了2次骰子,棋子才到达顶点B的概率;
(Ⅱ)记投了n次骰子,棋子在顶点B的概率为 .求
.求 .
.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖北省孝感高中高二(下)期末数学试卷(理科)(解析版) 题型:解答题
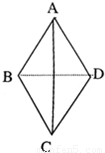
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com