练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若“0<x<1”是“(x-a)[x-(a+2)]≤0”的充分不必要条件,则实数a的取值范围是(　　)

    A.(-∞,0]∪[1,+∞)      B.(-1,0)

    C.[-1,0]                        D.(-∞,-1)∪(0,+∞)

    C.(x-a)[x-(a+2)]≤0⇒a≤x≤a+2,

    由集合的包含关系知:⇒a∈[-1,0].

    【方法总结】根据充要性求参数取值范围的策略

    (1)简化条件与结论.

    (2)根据条件与结论的关系,得到集合间的包含关系.

    (3)根据集合间的包含关系列不等式(组)求解.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

    已知a>0，函数，xÎ0，¥．设0<x2<，记曲线yfx在点Mx1，fx1处的切线为l．

    （1）　　   求l的方程；

    （2）　　   设l与x轴的交点为x2，0，证明：（i）0<x£；（ii）若x2<，则x1<x2<．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年重庆市七校联盟高三上学期联考理科数学试卷（解析版） 题型：选择题

    下列说法错误的是 (     )

    A．命题“若x2—4x+3=0,则x=3”的逆否命题是“若x≠3,则x2-4x+3≠0”

    B．“x>l”是“|x|>0”的充分不必要条件

    C．若p∧q为假命题,则p、g均为假命题

    D．命题P:“,使得x2+x+1<0”,则

     

    查看答案和解析>>

    科目：高中数学 来源：2014届黑龙江省高二下学期期末考试理科数学卷（解析版） 题型：解答题

    在直角坐标系xOy中,直线l的参数方程为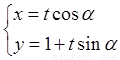(t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.

    (1)求直线l与曲线C的平面直角坐标方程;

    (2)设直线l与曲线C交于不同的两点A、B,若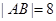,求α的值.

     

    查看答案和解析>>

    科目：高中数学 来源：2014届黑龙江省高二下学期期末考试文科数学卷（解析版） 题型：解答题

    在直角坐标系xOy中,直线l的参数方程为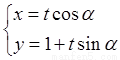(t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.

    (1)求直线l与曲线C的平面直角坐标方程;

    (2)设直线l与曲线C交于不同的两点A、B,若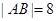,求α的值.

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河南省豫东、豫北十所名校高三测试理科数学试卷（解析版） 题型：解答题

    定义：已知函数f（x）与g（x），若存在一条直线y=kx +b，使得对公共定义域内的任意实数均满足g（x）≤f（x）≤kx+b恒成立，其中等号在公共点处成立，则称直线y=kx +b为曲线f（x）与g（x）的“左同旁切线”．已知

        （I）证明：直线y=x-l是f（x）与g（x）的“左同旁切线”；

        （Ⅱ）设P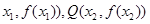（是函数 f（x）图象上任意两点，且0<x1<x2，若存在实数x3>0，使得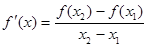．请结合（I）中的结论证明：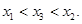

     

    查看答案和解析>>

    同步练习册答案