【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，下表记录了小李某月1号到5号每天打篮球时间
（单位：小时）与当天投篮命中率
之间的关系：
时间 | 1 | 2 | 3 | 4 | 5 |
命中率 | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
小李这5天的平均投篮命中率；用线性回归分析的方法，预测小李该月6号打6小时篮球的投篮命中率．
附：线性回归方程
中系数计算公式
， 
，
【答案】预测小李该月6号打6小时篮球的投篮命中率为
【解析】试题分析：（1）先求出小李这
天的平均投篮命中率，从而可得样本中心点的坐标，利用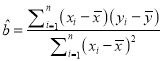
求出
，样本中心点的坐标代入回归方程可求得
，进而求出线性回归方程，先再令
，即可预测小李该月
号打
小时篮球的投篮命中率.
试题解析：小李这5天的平均投篮命中率
,
，
， 
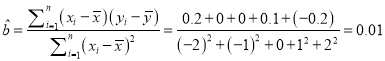∴线性回归方程
，则当
时， 
∴预测小李该月6号打6小时篮球的投篮命中率为
.
【方法点晴】本题主要考查散点图的画法和线性回归方程，属于难题.求回归直线方程的步骤：①依据样本数据画出散点图，确定两个变量具有线性相关关系；②计算
的值；③计算回归系数
；④写出回归直线方程为
；(2) 回归直线过样本点中心
是一条重要性质，利用线性回归方程可以估计总体，帮助我们分析两个变量的变化趋势.
科目：高中数学 来源： 题型：
【题目】已知
为定义在R上的奇函数，当
时，为二次函数，且满足
，
在
上的两个零点为
和
．
（1）求函数在R上的解析式；
（2）作出的图象，并根据图象讨论关于
的方程
根的个数．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随着网络的发展，人们可以在网络上购物、玩游戏、聊天、导航等，所以人们对上网流量的需求越来越大．某电信运营商推出一款新的“流量包”套餐．为了调查不同年龄的人是否愿意选择此款“流量包”套餐，随机抽取50个用户，按年龄分组进行访谈，统计结果如右表．
组 号 | 年龄 | 访谈 人数 | 愿意 使用 |
1 | [18，28） | 4 | 4 |
2 | [28，38） | 9 | 9 |
3 | [38，48） | 16 | 15 |
4 | [48，58） | 15 | 12 |
5 | [58，68） | 6 | 2 |
（Ⅰ）若在第2、3、4组愿意选择此款“流量包”套餐的人中，用分层抽样的方法抽取12人，则各组应分别抽取多少人？
（Ⅱ）若从第5组的被调查者访谈人中随机选取2人进行追踪调查，求2人中至少有1人愿意选择此款“流量包”套餐的概率．
（Ⅲ）按以上统计数据填写下面2×2列联表，并判断以48岁为分界点，能否在犯错误不超过1％的前提下认为，是否愿意选择此款“流量包”套餐与人的年龄有关？
年龄不低于48岁的人数 | 年龄低于48岁的人数 | 合计 | |
愿意使用的人数 | |||
不愿意使用的人数 | |||
合计 |
参考公式：
，其中：n＝a＋b＋c＋d．
P（k2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】祖暅原理：“幂势既同，则积不容异”．它是中国古代一个涉及几何体体积的问题，意思是两个同高的几何体，如在等高处的截面积恒相等，则体积相等．设
为两个同高的几何体，
的体积不相等，
在等高处的截面积不恒相等，根据祖暅原理可知，
是
的（ ）
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法：
①将一组数据中的每个数据都加上或减去同一个常数后，均值与方差都不变；
②设有一个回归方程
，变量x增加一个单位时，y平均增加3个单位；
③线性回归方程
必经过点
；
④在吸烟与患肺病这两个分类变量的计算中，从独立性检验知，有99％的把握认为吸烟与患肺病有关系时，我们说现有100人吸烟，那么其中有99人患肺病．其中错误的个数是（ ）
A. 0
B. 1
C. 2
D. 3
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设命题p:f(x)=2/(x-m)在区间(1,+∞)上是减函数;；命题q:2x-1+2m>0对任意x∈R恒成立.若(
p)∧q为真,求实数m的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
