
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
若平面α∥平面β,点A,C∈α,B,D∈β,则直线AC∥BD的充要条件是( )
(A)AB∥CD (B)AD∥CB
(C)AB与CD相交 (D)A,B,C,D共面
查看答案和解析>>
科目:高中数学 来源: 题型:
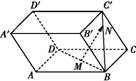
已知各个面都是平行四边形的四棱柱ABCD A′B′C′D′.设M是底面ABCD的中心,N是侧面BCC′B′的对角线BC′上的点,且BN∶
A′B′C′D′.设M是底面ABCD的中心,N是侧面BCC′B′的对角线BC′上的点,且BN∶
NC′=3∶1,设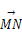 =α
=α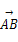 +β
+β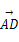 +γ
+γ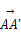 ,试求α,β,γ之值.
,试求α,β,γ之值.
查看答案和解析>>
科目:高中数学 来源: 题型:
将正方形ABCD沿对角线BD折成直二面角A BD
BD C,则下面结论错误的为( C )
C,则下面结论错误的为( C )
(A)AC⊥BD
(B)△ACD是等边三角形
(C)AB与平面BCD所成的角为60°
(D)AB与CD所成的角为60°
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点P(x0,y0),圆O:x2+y2=r2(r>0),直线l:x0x+y0y=r2,有以下几个结论:①若点P在圆O上,则直线l与圆O相切;②若点P在圆O外,则直线l与圆O相离;③若点P在圆O内,则直线l与圆O相交;④无论点P在何处,直线l与圆O恒相切.其中正确结论的个数是( )
A.1 B.2
C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆C:x2+(y-2)2=5,直线l:mx-y+1=0.
(1)求证:对m∈R,直线l与圆C总有两个不同的交点;
(2)若圆C与直线l交于A,B两点,求弦AB的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
若△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,则( )
A.△A1B1C1和△A2B2C2都是锐角三角形
B.△A1B1C1和△A2B2C2都是钝角三角形
C.△A1B1C1是钝角三角形,△A2B2C2是锐角三角形
D.△A1B1C1是锐角三角形,△A2B2C2是钝角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
一个几何体的三视图及其尺寸如图K405所示(单位:cm),其中主视图是直角三角形,左视图是半圆,俯视图是等腰三角形,则这个几何体的体积是( )
 D.π cm
D.π cm
3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com