
【题目】设椭圆![]()
![]() 的右焦点为
的右焦点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,假设
,假设![]() (其中
(其中![]() 为坐标原点)
为坐标原点)
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 上的任意一点,
上的任意一点,![]() 为圆
为圆![]() 的任意一条直径(
的任意一条直径(![]() 、
、![]() 为直径的两个端点),求
为直径的两个端点),求![]() 的最大值
的最大值
【答案】(1)![]() (2)11
(2)11
【解析】
(1)先求出![]() 坐标,再由
坐标,再由![]() ,联立求解,即可求得
,联立求解,即可求得![]() ,进而求得标准方程;
,进而求得标准方程;
(2)解法不唯一,可采用方法1中的向量法进行转化;也可采用方法2,纯代数运算,分别表示出点![]() ,其中
,其中![]() 的中点坐标为
的中点坐标为![]() ,可得
,可得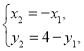 ,再表示出
,再表示出![]() 的坐标表达式,结合二次函数最值可求解;还可采用分类讨论直线斜率是否存在的方法,求出直线与圆的点坐标
的坐标表达式,结合二次函数最值可求解;还可采用分类讨论直线斜率是否存在的方法,求出直线与圆的点坐标![]() ,再结合
,再结合![]() 的坐标运算及二次函数性质即可求解;
的坐标运算及二次函数性质即可求解;
(1)由题设知,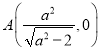 ,
,![]() ,由
,由![]() ,得
,得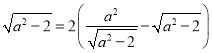 解得
解得![]() 、因此椭圆
、因此椭圆![]() 的方程为
的方程为![]() ;
;
(2)方法1:设圆![]() 的圆心为
的圆心为![]() ,
,
那么![]()
![]()
![]() ,
,
从而求![]() 的最大值转化为求
的最大值转化为求![]() 的最大值,
的最大值,
因为![]() 是椭圆
是椭圆![]() 上的任意一点,设
上的任意一点,设![]() ,因此
,因此![]() ,即
,即![]() ,
,
因为![]() ,因此
,因此![]() ,
,
因为![]() ,因此当
,因此当![]() 时,
时,![]() 取得最大值12,
取得最大值12,
因此![]() 的最大值为11;
的最大值为11;
方法2:设点![]() ,
,
因为![]() 的中点坐标为
的中点坐标为![]() ,因此
,因此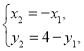
因此![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
因为点![]() 在圆
在圆![]() 上,因此
上,因此![]() ,即
,即![]() ,
,
因为点![]() 在椭圆
在椭圆![]() 上,因此
上,因此![]() ,即
,即![]() ,
,
因此![]()
![]()
![]() ,
,
因为![]() ,因此当
,因此当![]() 时,
时,![]() ;
;
方法3:①假设直线![]() 的斜率存在,设
的斜率存在,设![]() 的方程为
的方程为![]() ,
,
由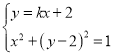 ,解得
,解得![]() ,
,
因为![]() 是椭圆
是椭圆![]() 上的任一点,设点
上的任一点,设点![]() ,
,
因此![]() ,即
,即![]() ,
,
因此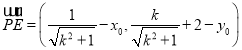 ,
,
因此![]() ,
,
因为![]() ,因此当
,因此当![]() 时,
时,![]() 取得最大值11;
取得最大值11;
②假设直线![]() 的斜率不存在,则
的斜率不存在,则![]() 的方程为
的方程为![]() ,
,
由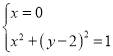 ,解得
,解得![]() 或
或![]() ,
,
不妨设,![]() ,
,![]() ,
,
因为![]() 是椭圆
是椭圆![]() 上的任一点,设点
上的任一点,设点![]() ,
,
因此![]() ,即
,即![]() ,
,
因此![]() ,
,![]() ,
,
因此![]() ,
,
因为![]() ,因此当
,因此当![]() 时,
时,![]() 取得最大值11,
取得最大值11,
综上可知,![]() 的最大值为11
的最大值为11


科目:高中数学 来源: 题型:
【题目】某校高三年级有1000名学生,其中理科班学生占80%,全体理科班学生参加一次考试,考试成绩近似地服从正态分布N(72,36),若考试成绩不低于60分为及格,则此次考试成绩及格的人数约为( )
(参考数据:若Z~N(μ,σ2),则P(μ﹣σ<Z≤μ+σ)=0.6826,P(μ﹣2σ<Z<μ+2σ)=0.9544,P(μ﹣3σ<Z<μ+3σ)=0.9974)
A.778B.780C.782D.784
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() ,
,![]() 为参数
为参数![]() ,在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线
,在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() Ⅰ
Ⅰ![]() 写出
写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
![]() Ⅱ
Ⅱ![]() 若
若![]() 与
与![]() 相交于A,B两点,求
相交于A,B两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的两个焦点分别为
的两个焦点分别为![]() 和
和![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() 和
和![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且满足
上,且满足![]() ,当
,当![]() 变化时,给出下列三个命题:
变化时,给出下列三个命题:
①点![]() 的轨迹关于
的轨迹关于![]() 轴对称;②
轴对称;②![]() 的最小值为2;
的最小值为2;
③存在![]() 使得椭圆
使得椭圆![]() 上满足条件的点
上满足条件的点![]() 仅有两个,
仅有两个,
其中,所有正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是由
是由![]() 个有序实数构成的一个数组,记作:
个有序实数构成的一个数组,记作:![]() .其中
.其中![]() 称为数组
称为数组![]() 的“元”,
的“元”,![]() 称为
称为![]() 的下标,如果数组
的下标,如果数组![]() 中的每个“元”都是来自数组
中的每个“元”都是来自数组![]() 中不同下标的“元”,则称
中不同下标的“元”,则称![]() 为
为![]() 的子数组.定义两个数组
的子数组.定义两个数组![]() ,
,![]() 的关系数为
的关系数为![]() .
.
(1)若![]() ,
,![]() ,设
,设![]() 是
是![]() 的含有两个“元”的子数组,求
的含有两个“元”的子数组,求![]() 的最大值;
的最大值;
(2)若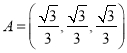 ,
,![]() ,且
,且![]() ,
,![]() 为
为![]() 的含有三个“元”的子数组,求
的含有三个“元”的子数组,求![]() 的最大值;
的最大值;
(3)若数组![]() 中的“元”满足
中的“元”满足![]() ,设数组
,设数组![]() 含有四个“元”
含有四个“元”![]() ,且
,且![]() ,求
,求![]() 与
与![]() 的所有含有三个“元”的子数组的关系数
的所有含有三个“元”的子数组的关系数![]() (
(![]() )的最大值.
)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1:![]() ,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C2是圆心极坐标为(3,π),半径为1的圆.
,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C2是圆心极坐标为(3,π),半径为1的圆.
(1)求曲线C1的参数方程和C2的直角坐标方程;
(2)设M,N分别为曲线C1,C2上的动点,求|MN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为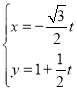 ,(t为参数)以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2
,(t为参数)以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2![]() sinθ,
sinθ,
(1)求直线l的普通方程及曲线C的直角坐标方程;
(2)直线l与x轴交于点P,与曲线C交于A,B两点,求|PA|+|PB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com