若a.b.cÎR+.且a+b+c=1.求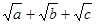的最大值．题目和参考答案——青夏教育精英家教网—

若a，b，cÎR⁺，且a+b+c=1，求的最大值．

解析试题分析：解：∵()²=a+b+c+2()         3分
≤1+2()=1+2(a+b+c)=3．           6分
∴，当且仅当a=b=c=时取“=”号．      8分
考点：不等式的求解最值
点评：主要是考查了运用均值不等式来求解最值，属于基础题

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

某厂家拟在2013年举行促销活动，经调查测算，该产品的年销售量（即该厂的年产量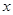）万件与年促销费用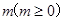万元满足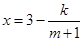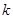（为常数），如果不搞促销活动，则该产品的年销售量是1万件. 已知2013年生产该产品的固定投入为8万元，每生产1万件该产品需要再投入16万元，厂家将每件产品的销售价格定为每件产品年平均成本的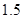倍（产品成本包括固定投入和再投入两部分资金，不包括促销费用）．
（1）将2013年该产品的利润万元表示为年促销费用万元的函数；
（2）该厂家2013年的促销费用投入多少万元时，厂家的利润最大？

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

某工厂拟建一座平面图为矩形，面积为的三段式污水处理池，池高为1，如果池的四周墙壁的建造费单价为元，池中的每道隔墙厚度不计，面积只计一面，隔墙的建造费单价为元，池底的建造费单价为元，则水池的长、宽分别为多少米时，污水池的造价最低？最低造价为多少元？

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

在矩形ABCD中，|AB|=2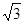，|AD|=2，E、F、G、H分别为矩形四条边的中点，以HF、GE所在直线分别为x，y轴建立直角坐标系(如图所示)．若R、R′分别在线段0F、CF上，且.

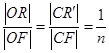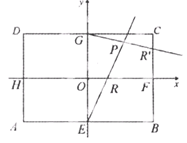
(Ⅰ)求证：直线ER与GR′的交点P在椭圆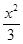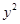：+=1上；
(Ⅱ)若M、N为椭圆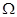上的两点，且直线GM与直线GN的斜率之积为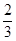，求证：直线MN过定点；并求△GMN面积的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

求证：

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

某食品厂定期购买面粉，已知该厂每天需要面粉6吨，每吨面粉的价格为3200元，面粉的保管等其它费用为平均每吨每天3元，购买面粉每次需要支付运费900元。
（Ⅰ）求该厂每隔多少天购买一次面粉，才能使平均每天支付的总费用最少？最少费用为多少？
（Ⅱ）某提供面粉的公司规定：当一次购买面粉不少于120吨时，价格可享受9.5折优惠，问该厂是否考虑利用此优惠条件？请说明理由。