
【题目】已知各项均为正数的等比数列{an}的首项a1=2,Sn为其前n项和,若5S1 , S3 , 3S2成等差数列.
(1)求数列{an}的通项公式;
(2)设bn=log2an , cn= ![]() ,记数列{cn}的前n项和为Tn . 若对于任意的n∈N* , Tn≤λ(n+4)恒成立,求实数λ的取值范围.
,记数列{cn}的前n项和为Tn . 若对于任意的n∈N* , Tn≤λ(n+4)恒成立,求实数λ的取值范围.
【答案】
(1)解:设{an}的公比为q.
∵5S1,S3,3S2成等差数列,∴2S3=5S1+3S2.
即 ![]() ,化简得2q2﹣q﹣6=0,
,化简得2q2﹣q﹣6=0,
解得:q=2或 ![]() .由已知,q=2.∴
.由已知,q=2.∴ ![]()
(2)解:由bn=log2an得 ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
∴ 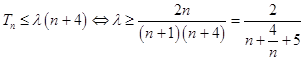
∵ ![]() ,当且仅当
,当且仅当 ![]() 即n=2时等号成立,
即n=2时等号成立,
∴ 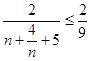 .
.
∴实数λ的取值范围是 ![]()
【解析】(1)由5S1 , S3 , 3S2成等差数列,利用性质建立方程,再用首项与公比将此方程转化为关于公比的等式,解出公比的值得出通项;(2)依次求出bn、cn , 根据所得出的形式,裂项求和即可.
【考点精析】根据题目的已知条件,利用数列的前n项和和等比数列的基本性质的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系 ;{an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列.
;{an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列.


科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x﹣1.
(1)求f(3)+f(﹣1);
(2)求f(x)的解析式;
(3)若x∈A,f(x)∈[﹣7,3],求区间A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题
(1)从0,1,2,3,4,5这六个数字任取3个,问能组成多少个没有重复数字的三位数?
(2)若(x6+3)(x2+ ![]() )5的展开式中含x10项的系数为43,求实数a的值.
)5的展开式中含x10项的系数为43,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网上叫外卖也开始成为不少人日常生活中不可或缺的一部分.为了解网络外卖在![]() 市的普及情况,
市的普及情况,![]() 市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到下表:(单位:人)
市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到下表:(单位:人)
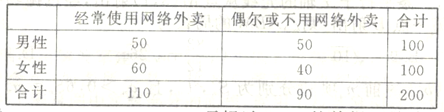
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用网络外卖的情况与性别有关?
市使用网络外卖的情况与性别有关?
(2)①现从所抽取的女网民中利用分层抽样的方法再抽取5人,再从这5人中随机选出3人赠送外卖优惠券,求选出的3人中至少有2人经常使用网络外卖的概率;
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c和一次函数g(x)=﹣bx,其中a,b,c∈R且满足a>b>c,f(1)=0.
(1)证明:函数f(x)与g(x)的图象交于不同的两点;
(2)若函数F(x)=f(x)﹣g(x)在[2,3]上的最小值为9,最大值为21,试求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+2x+c(a、c∈N*)满足:①f(1)=5;②6<f(2)<11.
(1)求a、c的值;
(2)若对任意的实数x∈[ ![]() ,
, ![]() ],都有f(x)﹣2mx≤1成立,求实数m的取值范围.
],都有f(x)﹣2mx≤1成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com