
若函数 满足:集合
满足:集合 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数 是等比源函数.
是等比源函数.
(Ⅰ)判断下列函数:①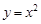 ;②
;② ;③
;③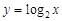 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(Ⅱ)判断函数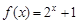 是否为等比源函数,并证明你的结论;
是否为等比源函数,并证明你的结论;
(Ⅲ)证明: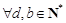 ,函数
,函数 都是等比源函数.
都是等比源函数.
(Ⅰ)①②③(Ⅱ)不是等比源函数(Ⅲ)略
【解析】
试题分析:(Ⅰ)① 是等比源函数,例:当
是等比源函数,例:当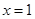 时,
时,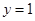 ;当
;当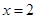 时,
时,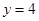 ;当
;当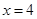 时,
时,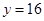 。1、4、16成等比。②
。1、4、16成等比。② 是等比源函数,例:当
是等比源函数,例:当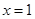 时,
时,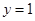 ;当
;当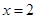 时,
时,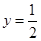 ;当
;当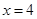 时,
时,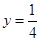 。
。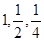 成等比。③
成等比。③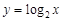 是等比源函数,例:当
是等比源函数,例:当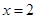 时,
时,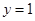 ;当
;当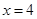 时,
时,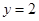 ;当
;当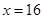 时,
时,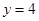 。1、2、4成等比数列。(Ⅱ)假设函数
。1、2、4成等比数列。(Ⅱ)假设函数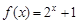 是等比源函数,即存在正整数
是等比源函数,即存在正整数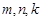 且
且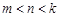 ,使得
,使得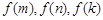 成等比数列,根据等比中项列出式子,再推理论证得出矛盾。(Ⅲ)根据
成等比数列,根据等比中项列出式子,再推理论证得出矛盾。(Ⅲ)根据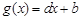 可推导出
可推导出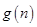 为首项为正整数公差也为正整数的等差数列。假设
为首项为正整数公差也为正整数的等差数列。假设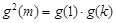 (
(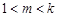 )整理得
)整理得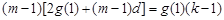 当
当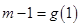 时说明假设成立,即函数
时说明假设成立,即函数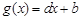 值中存在三个不同的数构成等比数列。
值中存在三个不同的数构成等比数列。
试题解析:(Ⅰ)①②③都是等比源函数. 3分
(Ⅱ)函数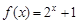 不是等比源函数.
4分
不是等比源函数.
4分
证明如下:
假设存在正整数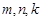 且
且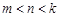 ,使得
,使得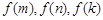 成等比数列,
成等比数列,
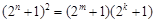 ,整理得
,整理得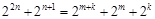 , 5分
, 5分
等式两边同除以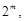 得
得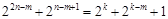 .
.
因为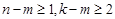 ,所以等式左边为偶数,等式右边为奇数,
,所以等式左边为偶数,等式右边为奇数,
所以等式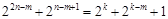 不可能成立,
不可能成立,
所以假设不成立,说明函数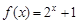 不是等比源函数. 8分
不是等比源函数. 8分
(Ⅲ)法1:
因为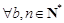 ,都有
,都有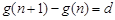 ,
,
所以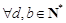 ,数列
,数列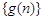 都是以
都是以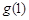 为首项公差为
为首项公差为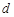 的等差数列.
的等差数列.
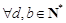 ,
,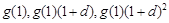 成等比数列,
成等比数列,
因为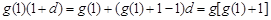 ,
,
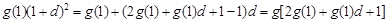 ,
,
所以
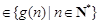 ,
,
所以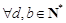 ,函数
,函数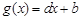 都是等比源函数.
13分
都是等比源函数.
13分
(Ⅲ)法2:
因为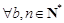 ,都有
,都有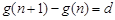 ,
,
所以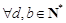 ,数列
,数列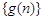 都是以
都是以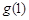 为首项公差为
为首项公差为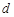 的等差数列.
的等差数列.
由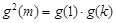 ,(其中
,(其中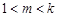 )可得
)可得
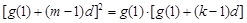 ,整理得
,整理得
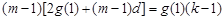 ,
,
令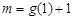 ,则
,则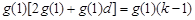 ,
,
所以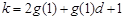 ,
,
所以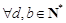 ,数列
,数列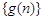 中总存在三项
中总存在三项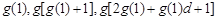 成等比数列.
成等比数列.
所以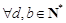 ,函数
,函数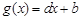 都是等比源函数.
13分
都是等比源函数.
13分
考点:新概念问题,考查分析能力、对所学知识的综合运用能力及论证推理能力。


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:2012-2013学年福建省、二中高三上学期期末联考理科数学卷(解析版) 题型:解答题
已知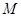 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意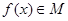 ,
,
① 方程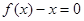 有实数根;② 函数
有实数根;② 函数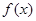 的导数
的导数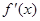 满足
满足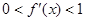 .
.
(Ⅰ)判断函数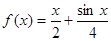 是否是集合
是否是集合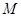 中的元素,并说明理由;
中的元素,并说明理由;
(Ⅱ)集合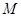 中的元素
中的元素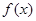 具有下面的性质:若
具有下面的性质:若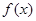 的定义域为
的定义域为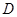 ,则对于任意
,则对于任意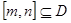 ,都存在
,都存在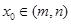 ,使得等式
,使得等式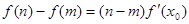 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程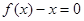 有且只有一个实数根;
有且只有一个实数根;
(Ⅲ)对任意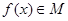 ,且
,且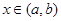 ,求证:对于
,求证:对于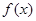 定义域中任意的
定义域中任意的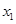 ,
,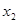 ,
,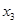 ,当
,当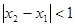 ,且
,且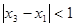 时,
时,
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市东城区高三上学期期末考试理科数学试卷(解析版) 题型:解答题
(本小题共14分)已知 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意 ,①方程
,①方程 有实数根;②函数
有实数根;②函数 的导数
的导数 满足
满足 .
.
(Ⅰ)判断函数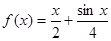 是否是集合
是否是集合 中的元素,并说明理由;
中的元素,并说明理由;
(Ⅱ)集合 中的元素
中的元素 具有下面的性质:若
具有下面的性质:若 的定义域为
的定义域为 ,则对于任意
,则对于任意 ,都存在
,都存在 ,使得等式
,使得等式 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程 有且只有一个实数根;
有且只有一个实数根;
(Ⅲ)对任意 ,且
,且 ,求证:对于
,求证:对于 定义域中任意的
定义域中任意的 ,
, ,
,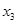 ,当
,当 ,且
,且 时,
时, .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市东城区高三上学期期末考试文科数学试卷(解析版) 题型:解答题
(本小题共14分)已知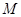 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意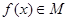 ,①方程
,①方程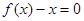 有实数根;②函数
有实数根;②函数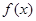 的导数
的导数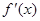 满足
满足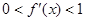 .
.
(Ⅰ)判断函数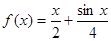 是否是集合
是否是集合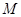 中的元素,并说明理由;
中的元素,并说明理由;
(Ⅱ)集合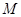 中的元素
中的元素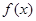 具有下面的性质:若
具有下面的性质:若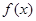 的定义域为
的定义域为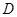 ,则对于任意
,则对于任意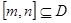 ,都存在
,都存在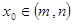 ,使得等式
,使得等式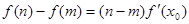 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程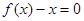 有且只有一个实数根;
有且只有一个实数根;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com