
已知函数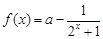 .
.
(1)确定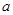 的值,使
的值,使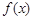 为奇函数;
为奇函数;
(2)当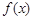 为奇函数时,求
为奇函数时,求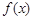 的值域。
的值域。
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1-m•2x |
| 1+m•2x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2+2x+1 |
| x2+1 |
| A、2 | ||
B、
| ||
| C、1 | ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
对于函数f(x),在使f(x)≤![]() M恒成立的所有常数M中,我们把M中的最小值称为函数f(x)的“上确界”.已知函数f(x)=
M恒成立的所有常数M中,我们把M中的最小值称为函数f(x)的“上确界”.已知函数f(x)=![]() +a(x∈[-2,2])是奇函数,则f(x)的上确界为( )
+a(x∈[-2,2])是奇函数,则f(x)的上确界为( )
A.2 B.![]()
C.1 D.![]()
查看答案和解析>>
科目:高中数学 来源:2013届浙江宁波四校高二下学期期中联考理科数学试卷(解析版) 题型:解答题
已知函数 , 其中
, 其中 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,求曲线
时,求曲线 的单调区间与极值.
的单调区间与极值.
【解析】第一问中利用当 时,
时, ,
,
 ,得到切线方程
,得到切线方程
第二问中,

对a分情况讨论,确定单调性和极值问题。
解: (1) 当 时,
时, ,
,
 ………………………….2分
………………………….2分

 切线方程为:
切线方程为:  …………………………..5分
…………………………..5分
(2) 
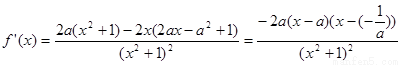 …….7
…….7 分
分
分类: 当 时, 很显然
时, 很显然
 的单调增区间为:
的单调增区间为:  单调减区间:
单调减区间:  ,
,
 ,
,  ………… 11分
………… 11分
当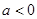 时
时 的单调减区间:
的单调减区间:  单调增区间:
单调增区间: 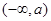 ,
,

 ,
, 
查看答案和解析>>
科目:高中数学 来源:台州一模 题型:单选题
| x2+2x+1 |
| x2+1 |
| A.2 | B.
| C.1 | D.
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com