
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA=45,点E、F分别为棱AB、PD的中点.

(1)求证:AF∥平面PCE;
(2)求三棱锥C-BEP的体积.
(1)详见解析;(2)三棱锥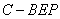 的体积为
的体积为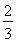 .
.
【解析】
试题分析:(1)求证: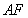 ∥平面
∥平面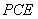 ,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,本题欲证
,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,本题欲证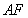 ∥平面
∥平面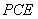 ,根据直线与平面平行的判定定理可知只需证
,根据直线与平面平行的判定定理可知只需证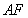 与平面
与平面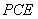 内一直线平行,取
内一直线平行,取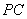 的中点
的中点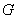 ,连接
,连接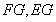 ,易证
,易证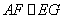 ,从而得
,从而得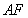 ∥平面
∥平面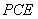 ;(2)求三棱锥
;(2)求三棱锥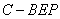 的体积,三棱锥
的体积,三棱锥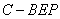 的体积可转化成三棱锥
的体积可转化成三棱锥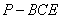 的体积,而
的体积,而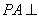 底面
底面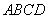 ,从而
,从而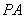 即为三棱锥
即为三棱锥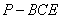 的高,根据三棱锥的体积公式进行求解即可.
的高,根据三棱锥的体积公式进行求解即可.
试题解析:(1)证明:取PC的中点G,连接GF,因为F为PD的中点,
所以,GF∥CD且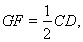 又E为AB的中点,ABCD是正方形,
又E为AB的中点,ABCD是正方形,
所以,AE∥CD且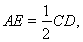 故AE∥GF且
故AE∥GF且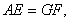
所以,AEGF是平行四边形,故AF∥EG,而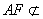 平面
平面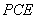 ,
,
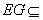 平面
平面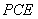 ,所以,AF∥平面
,所以,AF∥平面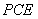 .
.
(2)因为PA⊥底面ABCD,所以,PA是三棱锥P-EBC的高,PA⊥AD,PA=2,
∠PDA=450,所以,AD=2,正方形ABCD中,E为AB的中点,所以,EB=1,故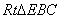 的面积为1,故
的面积为1,故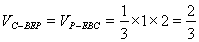 .
.
故三棱锥C-BEP的体积为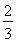 .
.
考点:直线与平面平行的判定;棱柱、棱锥、棱台的体积.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标2-1练习卷(解析版) 题型:填空题
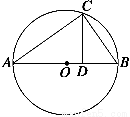
如图所示,AB为⊙O的直径,AC=4 cm,BC=3 cm,CD⊥AB于D,则CD的长为________ cm.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标1-1练习卷(解析版) 题型:填空题
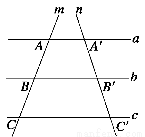
如图所示,已知a∥b∥c,直线m、n分别与a、b、c交于点A、B、C和A′、B′、C′,如果AB=BC=1,A′B′=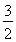 ,则B′C′=________.
,则B′C′=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西安第一中学高三第二学期第二次模拟考试理科数学试卷(解析版) 题型:选择题
设第一象限内的点 满足约束条件
满足约束条件 ,若目标函数
,若目标函数
 的最大值为40,则
的最大值为40,则 的最小值为( )
的最小值为( )
(A) (B)
(B) (C)1 (D)4
(C)1 (D)4
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西安第一中学高三第二学期第二次模拟考试文科数学试卷(解析版) 题型:选择题
直线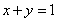 与圆
与圆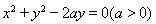 没有公共点,则
没有公共点,则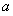 的取值范围是( )
的取值范围是( )
A.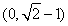 B.
B.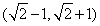 C.
C.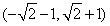 D.
D.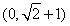
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com