
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,若
,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“类对称点”,当
的“类对称点”,当![]() 时,试问
时,试问![]() 是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为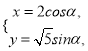 (
(![]() 为参数),以直角坐标系原点
为参数),以直角坐标系原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 距离的最大值及其对应的点
距离的最大值及其对应的点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大理石工厂初期花费98万元购买磨大理石刀具,第一年需要各种费用12万元,从第二年起,每年所需费用比上一年增加4万元,该大理石加工厂每年总收入50万元.
(1)到第几年末总利润最大,最大值是多少?
(2)到第几年末年平均利润最大,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在[﹣1,1]上的奇函数f(x),已知当x∈[﹣1,0]时的解析式f(x)= ![]() ﹣
﹣ ![]() (a∈R).
(a∈R).
(1)写出f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面![]() 平面
平面![]() ,
, ![]() 直线
直线![]() ,
, ![]() 是
是![]() 内不同的两点,
内不同的两点, ![]() 是
是![]() 内不同的两点,且
内不同的两点,且![]() 直线
直线![]() 上
上![]() 分别是线段
分别是线段![]() 的中点,下列判断正确的是( )
的中点,下列判断正确的是( )
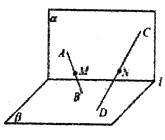
A. 当![]() 时,
时, ![]() 两点不可能重合
两点不可能重合
B. ![]() 两点可能重合,但此时直线
两点可能重合,但此时直线![]() 与
与![]() 不可能相交
不可能相交
C. 当![]() 与
与![]() 相交,直线
相交,直线![]() 平行于
平行于![]() 时,直线
时,直线![]() 可以与
可以与![]() 相交
相交
D. 当![]() 是异面直线时,直线
是异面直线时,直线![]() 可能与
可能与![]() 平行
平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]()
(1)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 两个不同点,求
两个不同点,求![]() 的最小值;
的最小值;
(2)直线![]() 上是否存在点
上是否存在点![]() ,满足经过点
,满足经过点![]() 有无数对互相垂直的直线
有无数对互相垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,并且直线
相交,并且直线![]() 被圆
被圆![]() 所截得的弦长等于直线
所截得的弦长等于直线![]() 被圆
被圆![]() 所截得的弦长?若存在,求出点
所截得的弦长?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关结论正确的个数为( )
①小赵、小钱、小孙、小李到4个景点旅游,每人只去一个景点,设事件![]() =“4个人去的景点不相同”,事件
=“4个人去的景点不相同”,事件![]() “小赵独自去一个景点”,则
“小赵独自去一个景点”,则![]() ;
;
②设函数![]() 存在导数且满足
存在导数且满足![]() ,则曲线
,则曲线![]() 在点
在点![]() 处的切线斜率为-1;
处的切线斜率为-1;
③设随机变量![]() 服从正态分布
服从正态分布![]() ,若
,若![]() ,则
,则![]() 与
与![]() 的值分别为
的值分别为![]() ;
;
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一个居民月用电量标准![]() ,用电量不超过
,用电量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以
的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
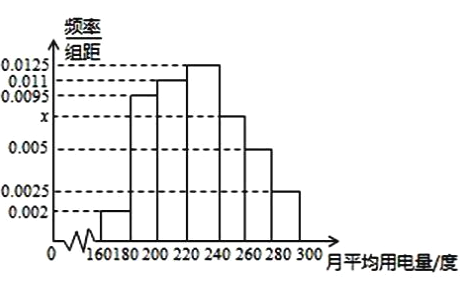
(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)如果当地政府希望使![]() 左右的居民每月的用电量不超出标准,根据样本估计总体的思想,你认为月用电量标准
左右的居民每月的用电量不超出标准,根据样本估计总体的思想,你认为月用电量标准![]() 应该定为多少合理?
应该定为多少合理?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为D的函数y=f(x),如果存在区间[m,n]D,同时满足:
①f(x)在[m,n]内是单调函数;
②当定义域是[m,n]时,f(x)的值域也是[m,n].
则称[m,n]是该函数的“和谐区间”.
(1)证明:[0,1]是函数y=f(x)=x2的一个“和谐区间”.
(2)求证:函数 ![]() 不存在“和谐区间”.
不存在“和谐区间”.
(3)已知:函数 ![]() (a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值.
(a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com