(1)一双曲线以椭圆16x2+25y2=400的焦点为顶点,椭圆的长轴端点为焦点,求双曲线的方程.
(2)若抛物线y2=2px(p>0)上一点A到准线及对称轴的距离分别为10和6,求A点的横坐标及抛物线的方程.
解:(1)∵椭圆16x
2+25y
2=400的标准形式为

∴椭圆的左右顶点坐标为(5,0)和(-5,0)
∵椭圆的半焦距c=

=3,
∴椭圆的焦点坐标为(3,0)和(-3,0)
∵双曲线的焦点是椭圆和左右顶点,顶点是椭圆的左右焦点
∴双曲线的b
2=25-9=16,可得双曲线的方程是:

-

=1;
(2)∵抛物线y
2=2px(p>0)上一点A到对称轴的距离为6,
∴设A(x
0,y
0),y
02=2px
0且|y
0|=6,可得2px
0=36…(*)
∵点A到准线的距离为10,
∴x
0+

=10,与(*)联解,可得
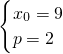
或
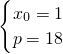
由此可得A点的横坐标为9,抛物线的方程是y
2=4x;或A点的横坐标为1,抛物线的方程是y
2=36x.
分析:(1)根据椭圆的基本概念,不难得到双曲线的顶点坐标和焦点坐标,再利用平方关系算出b的平方,即可得到所求双曲线的方程.
(2)设A(x
0,y
0),由抛物线上点A到对称轴的距离为6,得|y
0|=6.由此结合抛物线的标准方程和定义,建立x
0和p的方程组,解之即可得到A点的横坐标及抛物线的方程.
点评:本题第1问考查了椭圆、双曲线的标准方程与简单几何性质的知识;第2问考查了抛物线的定义与简单几何性质,两题都属于基础题.


 =3,
=3, -
- =1;
=1;  =10,与(*)联解,可得
=10,与(*)联解,可得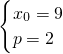 或
或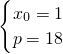


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案