
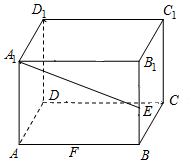
 已知在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点F是AB边上动点,点E是棱B1B的中点.
已知在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点F是AB边上动点,点E是棱B1B的中点.分析 (Ⅰ)推导出AB⊥A1D,AD1⊥A1D,从而A1D⊥平面ABD1,由此能证明D1F⊥A1D.
(Ⅱ)多面体ABCDED1的体积V=${V}_{{D}_{1}-ABCD}+{V}_{{D}_{1}-BCE}$,由此能求出结果.
解答 (本题满分12分)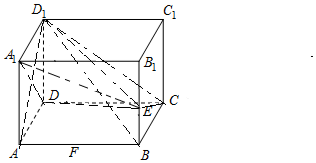
证明:(Ⅰ)∵在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,
∴AB⊥A1D,
∵四边形ADD1A1是正方形,∴AD1⊥A1D,
∵AB∩AD1=A,
∴A1D⊥平面ABD1,
∵点F是AB边上动点,∴D1F?平面ABD1,
∴D1F⊥A1D.
解:(Ⅱ)多面体ABCDED1的体积:
V=${V}_{{D}_{1}-ABCD}+{V}_{{D}_{1}-BCE}$
=$\frac{1}{3}×D{D}_{1}×{S}_{矩形ABCD}$+$\frac{1}{3}×AB×{S}_{△BCE}$
=$\frac{1}{3}×1×1×2+\frac{1}{3}×2×\frac{1}{2}×1×\frac{1}{2}$=$\frac{5}{6}$.
点评 本题考查线线垂直的证明,考查几何体体积的计算,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②④ | C. | ②⑤ | D. | ③⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,3] | B. | (2,3) | C. | (2,+∞) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 从某工厂生产的3000件产品中抽取600件进行质量检验 | |
| B. | 从某工厂生产的两箱(每箱15件)产品中抽取6件进行质量检验 | |
| C. | 从甲、乙两厂生产的两箱(每箱15件)产品中抽取6件进行质量检验 | |
| D. | 从某厂生产的3000件产品中抽取10件进行质量检验 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com