
 轴于点
轴于点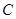 ,
,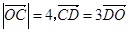 动点
动点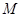 到直线
到直线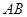 的距离是它到点
的距离是它到点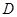 的距离的2倍.
的距离的2倍.
 的轨迹方程;
的轨迹方程; 为点
为点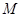 的轨迹与
的轨迹与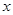 轴正半轴的交点,直线
轴正半轴的交点,直线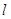 交点
交点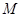 的轨迹于
的轨迹于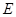 ,
,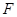 两点(
两点(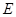 ,
,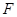 与点
与点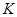 不重合),且满足
不重合),且满足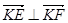 ,动点
,动点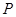 满足
满足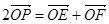 ,求直线
,求直线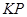 的斜率的取值范围.
的斜率的取值范围.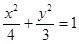

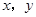 ),根据动点
),根据动点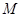 到直线
到直线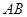 的距离是它到点
的距离是它到点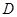 的距离的2倍,建立关于x,y的方程,然后化简整理可得所求动点M的轨迹方程.
的距离的2倍,建立关于x,y的方程,然后化简整理可得所求动点M的轨迹方程. 它与椭圆方程联立消y后得关于x的一元二次方程
它与椭圆方程联立消y后得关于x的一元二次方程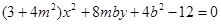 ,然后根据
,然后根据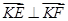 ,K点坐标为(2,0)
,K点坐标为(2,0)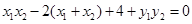 ,再借助直线方程和韦达定理建立m,b的方程,从而用m表示b,再代入直线方程可求出定点坐标.然后把KP的斜率表示成关于m的函数,利用函数的方法求其范围.
,再借助直线方程和韦达定理建立m,b的方程,从而用m表示b,再代入直线方程可求出定点坐标.然后把KP的斜率表示成关于m的函数,利用函数的方法求其范围. 得点D(-1,0)
得点D(-1,0)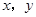 ),则:
),则:
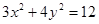
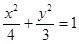
 代入
代入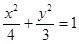 ,整理
,整理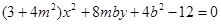
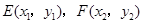
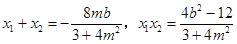

 ,K点坐标为(2,0)
,K点坐标为(2,0)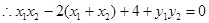 ,代入整理得
,代入整理得

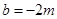 时,直线EF的方程为
时,直线EF的方程为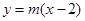 恒过点
恒过点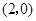 ,与已知矛盾,舍去.
,与已知矛盾,舍去.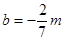 时,
时, ,由
,由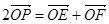 知
知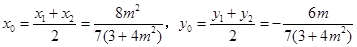

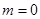 时,直线KP的斜率为0, 符合题意
时,直线KP的斜率为0, 符合题意 时,
时,
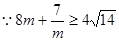
 时取“=”)或
时取“=”)或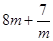 ≤-
≤- 时取“=”)
时取“=”) 或
或
 .
.

科目:高中数学 来源:不详 题型:解答题
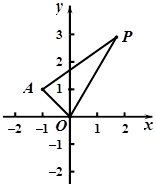
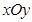 中,已知点
中,已知点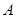
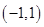 ,点P是动点,且三角形
,点P是动点,且三角形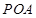 的三边所在直线
的三边所在直线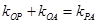 .
.
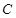 的方程;
的方程;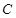 上异于点
上异于点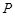 的一个点,若
的一个点,若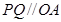 ,直线
,直线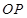 与
与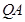 交于点M,探究是否存点P使得
交于点M,探究是否存点P使得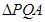 和
和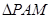 的面积满足
的面积满足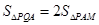 ,若存在,求出点P的坐标;若不存在,说明理由.
,若存在,求出点P的坐标;若不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com