解:(1)由题意得

,求得a=2,b=2

∴双曲线的方程为
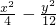
=1
(2)设直线的方程为x=ty+4,
由
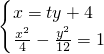
消去x得(3t
2-1)y
2+24ty+36=0
设M(x
1,y
1),N(x
2,y
2)
∴y
1+y
2=
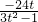
,y
1y
2=

∵直线l与双曲线右支相交,
∴x
1x
2=(ty
1+4)(ty
2+4)=t
2•

+4t•
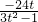
+16>0
∴
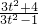
<0,t
2<

∴S
△BMN=

•|BF|•|y
1-y
2|=
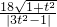
=36

∴t
2=

或

,∵t
2<

,∴t=±

∴直线l的方程为2x+y-8=0或2x-y-8=0
(3)∵点P为点M关于x轴的对称点,则p(x
1,-y
1),
∴

=(x
1-1,-y
1),
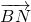
=(x
1,-y
1),
∵(x
1-1)y
2-(x
2-1)(-y
1)=2t•

+3•
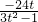
=0
∴

与
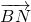
共线,
∴B,P,N三点共线.
分析:(1)把点A代入双曲线方程求得a和b的关系,进而根据焦点坐标求得c,可知a和b的另一关系式,联立求得a和b,则双曲线的方程可得.
(2)设直线方程,与双曲线方程联立消去x,设出M,N的坐标,根据韦达定理表示出y
1+y
2和y
1y
2,进而根据直线l与双曲线右支相交,
判断出x
1x
2<0求得t的范围,进而利用三角形面积公式表示出△BMN的面积求得t,则直线l的方程可得.
(3)根据点M的坐标表示出点P的坐标,进而分别表示出

和
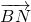
,进而求得

-
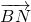
=0,判断出

和
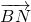
共线,进而推断出B,P,N三点共线.
点评:本土主要考查了直线与圆锥曲线的综合问题.考查了学生综合分析问题和基本的运算能力.

 =1(a>0,b>0)的一个焦点为F(4,0),直线l过点F且与双曲线右支交于点M、N,点B为双曲线右准线与x轴的交点.
=1(a>0,b>0)的一个焦点为F(4,0),直线l过点F且与双曲线右支交于点M、N,点B为双曲线右准线与x轴的交点. ,求直线l的方程;
,求直线l的方程; ,求得a=2,b=2
,求得a=2,b=2
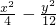 =1
=1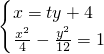 消去x得(3t2-1)y2+24ty+36=0
消去x得(3t2-1)y2+24ty+36=0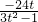 ,y1y2=
,y1y2=
 +4t•
+4t•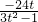 +16>0
+16>0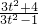 <0,t2<
<0,t2<
 •|BF|•|y1-y2|=
•|BF|•|y1-y2|=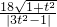 =36
=36
 或
或 ,∵t2<
,∵t2< ,∴t=±
,∴t=±
 =(x1-1,-y1),
=(x1-1,-y1),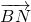 =(x1,-y1),
=(x1,-y1), +3•
+3•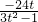 =0
=0 与
与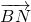 共线,
共线, 和
和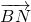 ,进而求得
,进而求得 -
-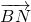 =0,判断出
=0,判断出 和
和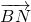 共线,进而推断出B,P,N三点共线.
共线,进而推断出B,P,N三点共线.

 名师点拨卷系列答案
名师点拨卷系列答案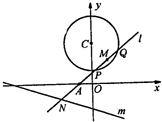 已知过点A(-1,0)的动直线l与圆C:x2+(y-3)2=4相交于P,Q两点,M是PQ中点,l与直线m:x+3y+6=0相交于N.
已知过点A(-1,0)的动直线l与圆C:x2+(y-3)2=4相交于P,Q两点,M是PQ中点,l与直线m:x+3y+6=0相交于N. 已知过点A(-1,0)的动直线l与圆C:x2+(y-3)2=4相交于P,Q两点,M是PQ的中点,l与直线m:x+3y+6=0相交于点N,则下面运算结果为定值的有( )
已知过点A(-1,0)的动直线l与圆C:x2+(y-3)2=4相交于P,Q两点,M是PQ的中点,l与直线m:x+3y+6=0相交于点N,则下面运算结果为定值的有( ) =1(a>0,b>0)的一个焦点为F(4,0),直线l过点F且与双曲线右支交于点M、N,点B为双曲线右准线与x轴的交点.
=1(a>0,b>0)的一个焦点为F(4,0),直线l过点F且与双曲线右支交于点M、N,点B为双曲线右准线与x轴的交点. ,求直线l的方程;
,求直线l的方程;