
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)若![]() 在
在![]() 上单调递増,求实数
上单调递増,求实数![]() 的取值范围;
的取值范围;
(2)若不等式![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出函数![]() 的导数
的导数![]() ,解不等式
,解不等式![]() 得出
得出![]() ,由题意得出
,由题意得出![]() ,列出不等式组求出实数
,列出不等式组求出实数![]() 的取值范围;
的取值范围;
(2)由![]() 可得
可得![]() 对任意的
对任意的![]() 恒成立,然后构造函数
恒成立,然后构造函数![]() ,将问题转化为
,将问题转化为![]() ,然后对实数
,然后对实数![]() 的取值进行分类讨论,确定函数
的取值进行分类讨论,确定函数![]() 在区间
在区间![]() 上的最小值
上的最小值![]() ,解出不等式
,解出不等式![]() 可得出实数
可得出实数![]() 的取值范围.
的取值范围.
(1)![]() ,
,
![]() .
.
解不等式![]() ,得
,得![]() .
.
由于函数![]() 在区间
在区间![]() 上单调递增,则
上单调递增,则![]() ,
,
所以![]() ,解得
,解得![]() ,因此,实数
,因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)不等式![]() 对任意的
对任意的![]() 恒成立,可得
恒成立,可得![]() 对任意的
对任意的![]() 恒成立,构造函数
恒成立,构造函数![]() ,其中
,其中![]() ,则
,则![]() .
.
![]() ,构造函数
,构造函数![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,则函数
,则函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
则![]() .
.
①当![]() 时,即当
时,即当![]() 时,对任意的
时,对任意的![]() ,
,![]() ,
,
此时,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() ,
,
解得![]() ,此时,
,此时,![]() ;
;
②当![]() 时,即当
时,即当![]() 时,则存在
时,则存在![]() ,使得
,使得![]() ,
,
此时,![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以,函数![]() 在
在![]() 处取得极小值,亦即最小值,
处取得极小值,亦即最小值,
即![]() ,
,
即![]() ,得
,得![]() ,又
,又![]() ,所以,
,所以,![]() ,解得
,解得![]() ,
,
此时![]() .
.
构造函数![]() ,其中
,其中![]() ,
,![]() ,此时,函数
,此时,函数![]() 单调递减,
单调递减,
所以,![]() ,即
,即![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】给出三个命题:①直线上有两点到平面的距离相等,则直线平行平面;②夹在两平行平面间的异面直线段的中点的连线平行于这个平面;③过空间一点必有唯一的平面与两异面直线平行.正确的是( )
A. ②③B. ①②C. ①②③D. ②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
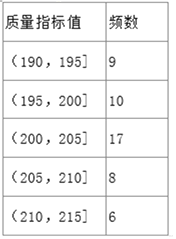
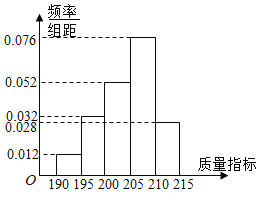
(1)根据频率分布直方图,估计乙流水线生产的产品该质量指标值的中位数;
(2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(3)根据已知条件完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲流水线 | 乙流水线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三角形ABE与菱形ABCD所在的平面互相垂直,![]() ,
,![]() ,M是AB的中点,N是CE的中点.
,M是AB的中点,N是CE的中点.
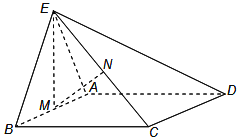
(1)求证:![]() ;
;
(2)求证:![]() 平面ADE;
平面ADE;
(3)求点A到平面BCE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() .
.
(1)求过点![]() 和函数
和函数![]() 的图像相切的直线方程;
的图像相切的直线方程;
(2)若对任意![]() ,有
,有![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若存在唯一的整数![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有![]() 两家大型石油炼化厂,这两家石油炼化厂所生产的成品油都要通过甲、乙两条输油管道输送到各地进行销售.由于地理位置及
两家大型石油炼化厂,这两家石油炼化厂所生产的成品油都要通过甲、乙两条输油管道输送到各地进行销售.由于地理位置及![]() 两家石油炼化厂的生产能力的不同,
两家石油炼化厂的生产能力的不同,![]() 石油炼化厂生产的成品油通过甲、乙两条输油管道输送时每吨的运费分别为1元和1.6元,
石油炼化厂生产的成品油通过甲、乙两条输油管道输送时每吨的运费分别为1元和1.6元,![]() 石油炼化厂生产的成品油通过甲、乙两条输油管道输送时每吨的运费分别为0.8元和1.5元.甲输油管道每年最多能输送290万吨成品油,乙输油管道每年最多能输送320万吨成品油.
石油炼化厂生产的成品油通过甲、乙两条输油管道输送时每吨的运费分别为0.8元和1.5元.甲输油管道每年最多能输送290万吨成品油,乙输油管道每年最多能输送320万吨成品油.![]() 石油炼化厂每年生产180万吨成品油,
石油炼化厂每年生产180万吨成品油,![]() 石油炼化厂每年生产240万吨成品油.规定
石油炼化厂每年生产240万吨成品油.规定![]() 石油炼化厂通过甲输油管道输送的成品油与
石油炼化厂通过甲输油管道输送的成品油与![]() 石油炼化厂通过甲输油管道输送的成品油的二倍之和不超过490万吨.问:两家炼化厂采用什么样的输油方案,能使总的运费最少?
石油炼化厂通过甲输油管道输送的成品油的二倍之和不超过490万吨.问:两家炼化厂采用什么样的输油方案,能使总的运费最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com