
【题目】某市有![]() 两家大型石油炼化厂,这两家石油炼化厂所生产的成品油都要通过甲、乙两条输油管道输送到各地进行销售.由于地理位置及
两家大型石油炼化厂,这两家石油炼化厂所生产的成品油都要通过甲、乙两条输油管道输送到各地进行销售.由于地理位置及![]() 两家石油炼化厂的生产能力的不同,
两家石油炼化厂的生产能力的不同,![]() 石油炼化厂生产的成品油通过甲、乙两条输油管道输送时每吨的运费分别为1元和1.6元,
石油炼化厂生产的成品油通过甲、乙两条输油管道输送时每吨的运费分别为1元和1.6元,![]() 石油炼化厂生产的成品油通过甲、乙两条输油管道输送时每吨的运费分别为0.8元和1.5元.甲输油管道每年最多能输送290万吨成品油,乙输油管道每年最多能输送320万吨成品油.
石油炼化厂生产的成品油通过甲、乙两条输油管道输送时每吨的运费分别为0.8元和1.5元.甲输油管道每年最多能输送290万吨成品油,乙输油管道每年最多能输送320万吨成品油.![]() 石油炼化厂每年生产180万吨成品油,
石油炼化厂每年生产180万吨成品油,![]() 石油炼化厂每年生产240万吨成品油.规定
石油炼化厂每年生产240万吨成品油.规定![]() 石油炼化厂通过甲输油管道输送的成品油与
石油炼化厂通过甲输油管道输送的成品油与![]() 石油炼化厂通过甲输油管道输送的成品油的二倍之和不超过490万吨.问:两家炼化厂采用什么样的输油方案,能使总的运费最少?
石油炼化厂通过甲输油管道输送的成品油的二倍之和不超过490万吨.问:两家炼化厂采用什么样的输油方案,能使总的运费最少?
【答案】![]() 石油炼化厂通过甲输油管道输送90万吨成品油,通过乙输油管道输送90万吨成品油,
石油炼化厂通过甲输油管道输送90万吨成品油,通过乙输油管道输送90万吨成品油,![]() 石油炼化厂通过甲输油管道输送200万吨成品油,通过乙输油管道输送40万吨成品油时,总运费最少.
石油炼化厂通过甲输油管道输送200万吨成品油,通过乙输油管道输送40万吨成品油时,总运费最少.
【解析】
根据题意设出未知数,设![]() 石油炼化厂通过甲输油管道输送
石油炼化厂通过甲输油管道输送![]() 万吨成品油,
万吨成品油,![]() 石油炼化厂通过甲输油管道输送
石油炼化厂通过甲输油管道输送![]() 万吨成品油,总运费为
万吨成品油,总运费为![]() 万元,列出不等式组及目标函数,利用数形结合求解出目标最小值时x、y值即可.
万元,列出不等式组及目标函数,利用数形结合求解出目标最小值时x、y值即可.
设![]() 石油炼化厂通过甲输油管道输送
石油炼化厂通过甲输油管道输送![]() 万吨成品油,
万吨成品油,![]() 石油炼化厂通过甲输油管道输送
石油炼化厂通过甲输油管道输送![]() 万吨成品油,总运费为
万吨成品油,总运费为![]() 万元,则
万元,则
![]() .
.
![]() 应满足
应满足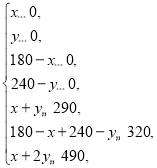 ,即
,即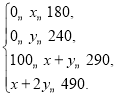
作出上面的不等式组所表示的平面区域,如图阴影部分所示:
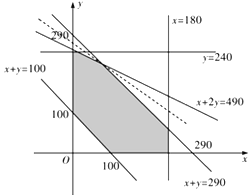
设直线![]() 与
与![]() 的交点为
的交点为![]() ,则
,则![]() .
.
把直线![]() 向上平移至经过平面区域上的点
向上平移至经过平面区域上的点![]() 时,
时,![]() 的值最小.
的值最小.
∵点![]() 的坐标为
的坐标为![]() ,
,
∴![]() 石油炼化厂通过甲输油管道输送90万吨成品油,通过乙输油管道输送90万吨成品油,
石油炼化厂通过甲输油管道输送90万吨成品油,通过乙输油管道输送90万吨成品油,![]() 石油炼化厂通过甲输油管道输送200万吨成品油,通过乙输油管道输送40万吨成品油时,总运费最少.
石油炼化厂通过甲输油管道输送200万吨成品油,通过乙输油管道输送40万吨成品油时,总运费最少.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣a)cosx﹣sinx,g(x)![]() x3
x3![]() ax2,a∈R
ax2,a∈R
(1)当a=1时,求函数y=f(x)在区间(0,![]() )上零点的个数;
)上零点的个数;
(2)令F(x)=f(x)+g(x),试讨论函数y=F(x)极值点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,梯形
中,梯形![]() 与平行四边形
与平行四边形![]() 所在平面互相垂直,
所在平面互相垂直, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)判断线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求 出
?若存在,求 出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某文体局为了解“跑团”每月跑步的平均里程,收集并整理了2018年1月至2018年11月期间“跑团”每月跑步的平均里程(单位:公里)的数据,绘制了下面的折线图.根据折线图,下列结论正确的是( )

A. 月跑步平均里程的中位数为6月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在8、9月
D. 1月至5月的月跑步平均里程相对于6月至11月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)。曲线
为参数)。曲线![]() 的参数方程为
的参数方程为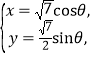 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,求
,求![]() 的面积(其中
的面积(其中![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|y=lg(x-![]() )},B={x|
)},B={x|![]() -cx<0,c>0},若AB,则实数c的取值范围是( )
-cx<0,c>0},若AB,则实数c的取值范围是( )
A.(0,1]B.[1,+∞)
C.(0,1)D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取了40辆汽车在经过路段上某点时的车速(km/h),现将其分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如图所示的频率分布直方图.
,后得到如图所示的频率分布直方图.
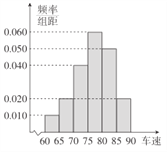
(Ⅰ)现有某汽车途经该点,则其速度低于80km/h的概率约是多少?
(Ⅱ)根据直方图可知,抽取的40辆汽车经过该点的平均速度约是多少?
(Ⅲ)在抽取的40辆且速度在![]() (km/h)内的汽车中任取2辆,求这2辆车车速都在
(km/h)内的汽车中任取2辆,求这2辆车车速都在![]() (km/h)内的概率.
(km/h)内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com