
一条变动的直线L与椭圆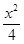 +
+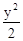 =1交于P、Q两点,M是L上的动点,满足关系|MP|·|MQ|=2.若直线L在变动过程中始终保持其斜率等于1.求动点M的轨迹方程,并说明曲线的形状.
=1交于P、Q两点,M是L上的动点,满足关系|MP|·|MQ|=2.若直线L在变动过程中始终保持其斜率等于1.求动点M的轨迹方程,并说明曲线的形状.
x2+2y2=1.
【解析】
试题分析:设动点M(x,y),动直线L:y=x+m,并设P(x1,y1),Q(x2,y2)是方程组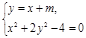 的解,消去y,得3x2+4mx+2m2-4=0,其中Δ=16m2-12(2m2-4)>0,∴-
的解,消去y,得3x2+4mx+2m2-4=0,其中Δ=16m2-12(2m2-4)>0,∴-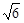 <m<
<m<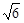 ,且x1+x2=-
,且x1+x2=-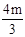 ,x1x2=
,x1x2=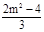 ,又∵|MP|=
,又∵|MP|=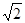 |x-x1|,|MQ|=
|x-x1|,|MQ|=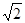 |x-x2|.由|MP||MQ|=2,得|x-x1||x-x2|=1,也即
|x-x2|.由|MP||MQ|=2,得|x-x1||x-x2|=1,也即
|x2-(x1+x2)x+x1x2|=1,于是有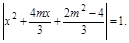 ∵m=y-x,∴|x2+2y2-4|=3.由x2+2y2-4=3,得椭圆
∵m=y-x,∴|x2+2y2-4|=3.由x2+2y2-4=3,得椭圆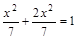 夹在直线
夹在直线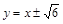 间两段弧,且不包含端点.由x2+2y2-4=-3,得椭圆x2+2y2=1.
间两段弧,且不包含端点.由x2+2y2-4=-3,得椭圆x2+2y2=1.
考点:本题主要考查直线和圆锥曲线的位置关系、轨迹方程的求法。
点评:解答中从联立方程组出发,运用韦达定理,体现了整体观,是解析几何问题中的常见类型。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(b>0)是圆的一条切线,且l与椭圆
如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(b>0)是圆的一条切线,且l与椭圆| x2 |
| 2 |
| 2 |
| 3 |
| ||
| 4 |
2
| ||
| 7 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆
如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆| x2 |
| 2 |
| 4 |
| 3 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
2
| ||
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•南宁模拟)已知椭圆W的中心在原点,焦点在x轴上,离心率为
(2012•南宁模拟)已知椭圆W的中心在原点,焦点在x轴上,离心率为
| ||
| 3 |
| CF |
| FB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com