
某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组 ,第2组
,第2组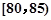 ,第3组
,第3组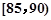 ,第4组
,第4组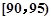 ,第5组
,第5组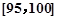 ,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
(Ⅰ)求出第4组的频率,并补全频率分布直方图;
(Ⅱ)根据样本频率分布直方图估计样本的中位数;
(Ⅲ)如果用分层抽样的方法从“优秀”和“良好” 的学生中共选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
(Ⅰ)0.2,图详见解析;(Ⅱ) ;(Ⅲ)
;(Ⅲ)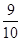
解析试题分析:在频率分布直方图中需要掌握①:每个小矩形的面积代表落在这个组内数据的频率,所有小矩形的面积和等于1,②利用频率分布直方图可以估计总体的数字特征:众数、中位数、平均数,其中众数是最高矩形的中点横坐标;中位数是两边矩形的面积和各为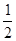 的分界点;平均数等于每个小矩形面积乘以中点横坐标的累加值,③落在每个小矩形内的数据是用其中点横坐标刻画的,(Ⅰ)根据频率和等于1,可计算第四组的频率,然后除以组距,就是这个组的高,即可补全频率分布直方图;(Ⅱ)设样本的中位数为
的分界点;平均数等于每个小矩形面积乘以中点横坐标的累加值,③落在每个小矩形内的数据是用其中点横坐标刻画的,(Ⅰ)根据频率和等于1,可计算第四组的频率,然后除以组距,就是这个组的高,即可补全频率分布直方图;(Ⅱ)设样本的中位数为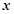 ,则
,则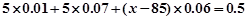 ,可计算
,可计算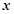 的值;(Ⅲ)根据分层抽样可计算出抽取的5人中,优秀3人,良好2人,从中选2人,共有10种结果,其中“全为良好”包括1种结果,∴
的值;(Ⅲ)根据分层抽样可计算出抽取的5人中,优秀3人,良好2人,从中选2人,共有10种结果,其中“全为良好”包括1种结果,∴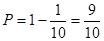 .
.
试题解析:(Ⅰ)其它组的频率为(0.01+0.07+0.06+0.02)×5=0.8,
所以第四组的频率为0.2,-----2分
频率/组距是0.04
频率分布图如图: 4分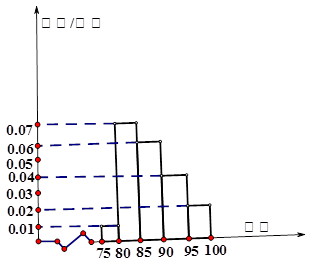
(Ⅱ)设样本的中位数为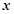 ,则
,则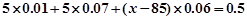 5分
5分
解得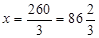
所以样本中位数的估计值为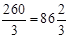 6分
6分
(Ⅲ)依题意良好的人数为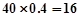 人,优秀的人数为
人,优秀的人数为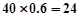 人抽取比例为1/8,所以采用分层抽样的方法抽取的5人中有优秀3人,良好2人 8分
人抽取比例为1/8,所以采用分层抽样的方法抽取的5人中有优秀3人,良好2人 8分
法1:记从这5人中选2人至少有1人是优秀为事件M
将考试成绩优秀的三名学生记为A,B,C, 考试成绩良好的两名学生记为a,b
从这5人中任选2人的所有基本事件包括:AB,AC,BC,Aa,Ab,Ba,Bb,Ca,Cb,ab
共10个基本事件 9分
事件M含的情况是:AB,AC,BC,Aa,Ab,Ba,Bb,Ca,Cb,共9个 10分
所以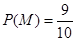 12分
12分
法2:P=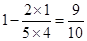
考点:1、频率分布直方图和应用;2、古典概型.


科目:高中数学 来源: 题型:解答题
 是指大气中直径小于或等于
是指大气中直径小于或等于 微米的颗粒物,也称为可吸入肺颗粒物.我国
微米的颗粒物,也称为可吸入肺颗粒物.我国 标准采用世卫组织设定的最宽限值,即
标准采用世卫组织设定的最宽限值,即 日均值在
日均值在 微克/立方米以下空气质量为一级;在
微克/立方米以下空气质量为一级;在 微克/立方米
微克/立方米 微克/立方米之间空气质量为二级;在
微克/立方米之间空气质量为二级;在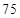 微克/立方米以上空气质量为超标.某试点城市环保局从该市市区
微克/立方米以上空气质量为超标.某试点城市环保局从该市市区 年上半年每天的
年上半年每天的 监测数据中随机的抽取
监测数据中随机的抽取 天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
(1)在这 天的
天的 日均监测数据中,求其中位数;
日均监测数据中,求其中位数;
(2)从这 天的数据中任取
天的数据中任取 天数据,记
天数据,记 表示抽到
表示抽到 监测数据超标的天数,求
监测数据超标的天数,求 的分布列及数学期望;
的分布列及数学期望;
(3)以这 天的
天的 日均值来估计一年的空气质量情况,则一年(按
日均值来估计一年的空气质量情况,则一年(按 天计算)中平均有多少天的空气质量达到一级或二级.
天计算)中平均有多少天的空气质量达到一级或二级.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如下表:
 | A | B | C |
| A | 7 | 20 | 5 |
| B | 9 | 18 | 6 |
| C | a | 4 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.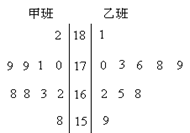
(1)根据茎叶图判断哪个班的平均身高较高;
(2)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如下茎叶图所示:
(Ⅰ)从甲、乙两人中选择1人参加数学趣味知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(II)从乙的6次培训成绩中随机选择2个,试求选到123分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(Ⅰ)根据以上数据建立一个2×2列联表;
(Ⅱ)试判断是否有97.5%的把握认为“休闲方式与性别有关”?
下面临界值表仅供参考:
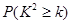 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
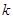 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
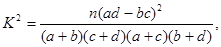 其中
其中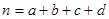 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分共12分)为了比较两种治疗失眠症的药(分别成为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者服用一段时间后,记录他们日平均增加的睡眠时间(单位:h)实验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5
2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4
1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5
(1)分别计算两组数据的平均数,从计算结果来看,哪种药的效果好?
(2)完成茎叶图,从茎叶图来看,哪种药疗效更好?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7、8、9、10环,且每次射击成绩互不影响,射击环数的频率分布表如下: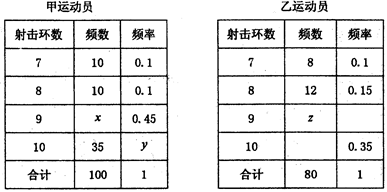
若将频率视为概率,回答下列问题:
(1)求表中x,y,z的值及甲运动员击中10环的概率;
(2)求甲运动员在3次射击中至少有一次击中9环以上(含9环)的概率;
(3)若甲运动员射击2次,乙运动员射击1次, 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求 的分布列及
的分布列及
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某初级中学共有学生2000名,各年级男、女生人数如下表:
| | 初一年级 | 初二年级 | 初三年级 |
| 女生 | 373 | 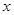 | 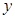 |
| 男生 | 377 | 370 | 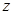 |
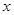 的值;
的值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com