
甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7、8、9、10环,且每次射击成绩互不影响,射击环数的频率分布表如下: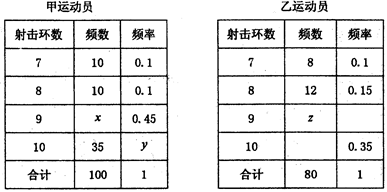
若将频率视为概率,回答下列问题:
(1)求表中x,y,z的值及甲运动员击中10环的概率;
(2)求甲运动员在3次射击中至少有一次击中9环以上(含9环)的概率;
(3)若甲运动员射击2次,乙运动员射击1次, 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求 的分布列及
的分布列及
(1)0.35;(2)0.992;(3)2.35,分布列如下:ξ 0 1 2 3 P 0.01 0.11 0.4 0. 48
解析试题分析:(1)结合频率分布表、频率之和为1的性质和频率的计算公式去求;(2)利用“至少有一次击中9环以上(含9环)”的对立事件是“三次都没有击中9环以上(含9环)”,而且三次射击的事件都是彼此相互独立的,所以“三次都没有击中9环以上(含9环)”的概率是0.23,再用间接法求.(3)先根据独立事件的乘法公式求出随机变量各取值的概率,再写出其分布列和数学期望.
试题解析:(1)由题意可得x=100(10+10+35)=45,y=1(0.1+0.1+0.45)=0.35,
因为乙运动员的射击环数为9时的频率为1(0.1+0.15+0.35)=0.4,所以z=0.4×80=32,
由上可得表中x处填45,y处填0.35,z处填32. 3分
设“甲运动员击中10环”为事件A,则P(A)=0.35,
即甲运动员击中10环的概率为0.35. 4分
(2)设甲运动员击中9环为事件A1,击中10环为事件A2,则甲运动员在一次射击中击中9
环以上(含9环)的概率为P(A1+A2)=P(A1)+P(A2)=0.45+0.35=0.8,
故甲运动员在3次射击中至少有一次击中9环以上(含9环)的概率
P=1[1P(A1+A2)]3=10.23=0.992 7分
(3)ζ的可能取值是0,1,2,3,则P(ζ=0)=0.22×0.25=0.01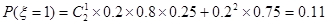
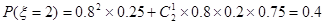
 10分
10分
所以ξ的分布列是ξ 0 1 2 3 P 0.01 0.11 0.4 0. 48 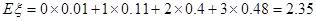 12分
12分
考点:1、随机变量概率分布列和数学期望的计算,2、互斥事件的概率,3、相互独立事件的概率.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图所示).已知图中从左到右的前3个小组的频率之比为1∶2∶3,第2小组的频数为12,求抽取的学生人数.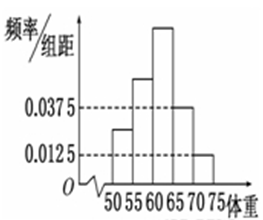
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组 ,第2组
,第2组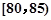 ,第3组
,第3组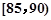 ,第4组
,第4组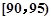 ,第5组
,第5组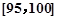 ,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
(Ⅰ)求出第4组的频率,并补全频率分布直方图;
(Ⅱ)根据样本频率分布直方图估计样本的中位数;
(Ⅲ)如果用分层抽样的方法从“优秀”和“良好” 的学生中共选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解今年某校高三毕业班准备报考飞行员学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为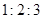 ,其中第二小组的频数为12.
,其中第二小组的频数为12.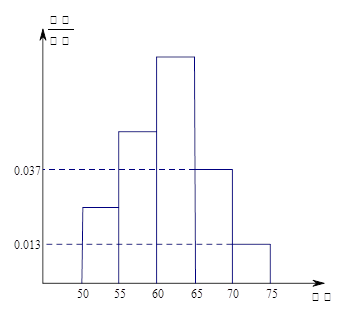
(1)求该校报考飞行员的总人数;
(2)以这所学校的样本来估计全省的总体数据,若从全省报考飞行员的同学中(人数很多)任选三人,设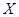 表示体重超过60公斤的学生人数,求
表示体重超过60公斤的学生人数,求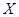 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取的20名学生的成绩进行分析,分数用茎叶图记录如下: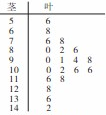
得到频率分步表如下:
(1)求表中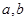 的值,并估计这次考试全校学生数学成绩及格率(分数在
的值,并估计这次考试全校学生数学成绩及格率(分数在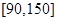 范围为及格);
范围为及格);
(2)从大于等于110分的学生中随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某学校高二年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
(1)完成下面的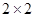 列联表;
列联表;
| | 不喜欢运动 | 喜欢运动 | 合计 |
| 女生 | 50 | | |
| 男生 | | | |
| 合计 | | 100 | 200 |
 和
和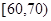 的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.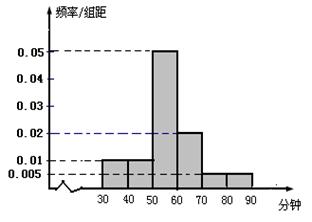
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,统计了他们的成绩,得到如图所示的频率分布直方图.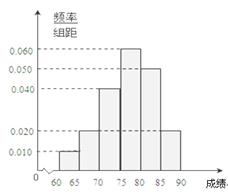
(Ⅰ)在这个调查采样中,用到的是什么抽样方法?
(Ⅱ)写出这40个考生成绩的众数、中位数(只写结果);
(Ⅲ)若从成绩在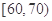 的考生中任抽取2人,求成绩在
的考生中任抽取2人,求成绩在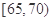 的考生至少有一人的概率.
的考生至少有一人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如右图所示.经销商为下一个销售季度购进了130t该农产品.以 (单位:t,100≤
(单位:t,100≤ ≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.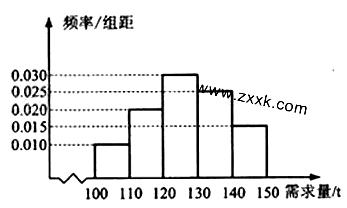
(Ⅰ)将T表示为 的函数;
的函数;
(Ⅱ)根据直方图估计利润T不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一段时间内,某种商品价格 (万元)和需求量
(万元)和需求量 之间的一组数据为:
之间的一组数据为:
价 格 | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量 | 12 | 10 | 7 | 5 | 3 |
 与
与 之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01
之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01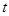 )
)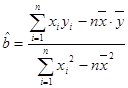 ,
,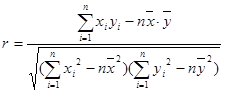 ,
,
| n-2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 小概率0.01 | 1.000 | 0.990 | 0.959 | 0.917 | 0.874 | 0.834 | 0.798 | 0.765 | 0.735 | 0.708 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com