
(本小题满分12分)
某学校高二年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
(1)完成下面的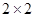 列联表;
列联表;
| | 不喜欢运动 | 喜欢运动 | 合计 |
| 女生 | 50 | | |
| 男生 | | | |
| 合计 | | 100 | 200 |
 和
和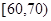 的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.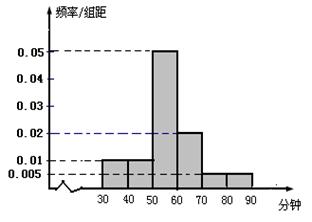
(1)列联表详见解析;(2)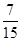 .
.
解析试题分析:(1)利用分层抽样填表;(2)利用频率分步直方图求出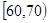 内的人数和在
内的人数和在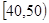 的人数,列出所有的情况,列出概率.
的人数,列出所有的情况,列出概率.
试题解析:(1)根据分层抽样的定义,知抽取男生130人,女生70人, 1分
3分 不喜欢运动 喜欢运动 合计 女生 50 20 70 男生 50 80 130 合计 100 100 200
(2)由直方图知在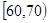 内的人数为4人,设为
内的人数为4人,设为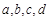 .
.
在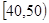 的人数为2人,设为
的人数为2人,设为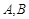 . 5分
. 5分
从这6人中任选2人有AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd,ab,ac,ad,bc,bd,cd
共15种情况 7分
若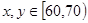 时,有
时,有 共六种情况. 9分
共六种情况. 9分
若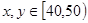 时,有
时,有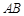 一种情况. 10分
一种情况. 10分
事件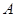 :“她们在同一区间段”所包含的基本事件个数有
:“她们在同一区间段”所包含的基本事件个数有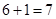 种, 11分
种, 11分
故 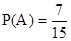
答:两名女生的运动时间在同一区间段的概率为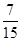 . 12分
. 12分
考点:1.分层抽样;2.频率分步直方图.


科目:高中数学 来源: 题型:解答题
某小区在一次对20岁以上居民节能意识的问卷调查中,随机抽取了100份问卷进行统计,得到相关的数据如下表: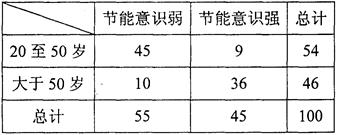
(Ⅰ)由表中数据直观分析,节能意识强弱是否与人的年龄有关?
(Ⅱ)据了解到,全小区节能意识强的人共有350人,估计这350人中,年龄大于50岁的有多少人?
(Ⅲ)按年龄分层抽样,从节能意识强的居民中抽5人,再从这5人中任取2人,求恰有1人年龄在20至50岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(Ⅰ)根据以上数据建立一个2×2列联表;
(Ⅱ)试判断是否有97.5%的把握认为“休闲方式与性别有关”?
下面临界值表仅供参考:
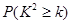 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
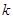 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
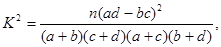 其中
其中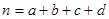 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学生社团在对本校学生学习方法开展问卷调查的过程中发现,在回收上来的1000份有效问卷中,同学们背英语单词的时间安排共有两种:白天背和晚上睡前背。为了研究背单词时间安排对记忆效果的影响,该社团以5%的比例对这1000名学生按时间安排类型进行分层抽样,并完成一项实验.实验方法是,使两组学生记忆40个无意义音节(如XIQ、GEH),均要求在刚能全部记清时就停止识记,并在8小时后进行记忆检测。不同的是,甲组同学识记结束后一直不睡觉,8小时后测验;乙组同学识记停止后立刻睡觉,8小时后叫醒测验.
两组同学识记停止8小时后的准确回忆(保持)情况如图(区间含左端点而不含右端点).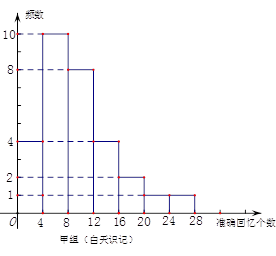
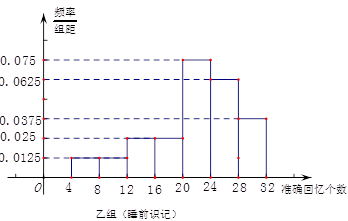
(1)估计这1000名被调查学生中停止后8小时40个音节的保持率不小于60%的人数;
(2)从乙组准确回忆单词个数在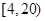 个范围内的学生中随机选2人,求能准确回忆
个范围内的学生中随机选2人,求能准确回忆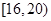 个单词至少有一人的概率.
个单词至少有一人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7、8、9、10环,且每次射击成绩互不影响,射击环数的频率分布表如下: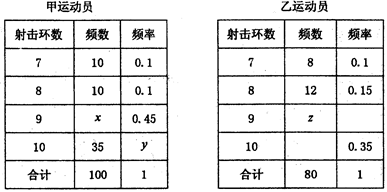
若将频率视为概率,回答下列问题:
(1)求表中x,y,z的值及甲运动员击中10环的概率;
(2)求甲运动员在3次射击中至少有一次击中9环以上(含9环)的概率;
(3)若甲运动员射击2次,乙运动员射击1次, 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求 的分布列及
的分布列及
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表是某单位在2013年1—5月份用水量(单位:百吨)的一组数据:
月份 | 1 | 2 | 3 | 4 | 5 |
用水量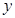 | 4 5 | 4 | 3 | 2 5 | 1 8 |
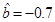 ,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;
,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;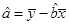 ,
,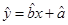
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2012年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类: 第一类的用电区间在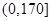 ,第二类在
,第二类在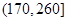 ,第三类在
,第三类在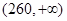 (单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
(单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
⑴ 求该小区居民用电量的中位数与平均数;
⑵ 本月份该小区没有第三类的用电户出现,为鼓励居民节约用电,供电部门决定:对第一类每户奖励20元钱,第二类每户奖励5元钱,求每户居民获得奖励的平均值;
⑶ 利用分层抽样的方法从该小区内选出5户居民代表,若从该5户居民代表中任选两户居民,求这两户居民用电资费属于不同类型的概率. 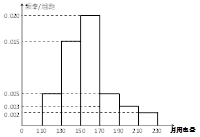
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
PM2. 5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物。我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米 75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
某试点城市环保局从该市市区2011年全年每天的PM2.5监测数据中随机的抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)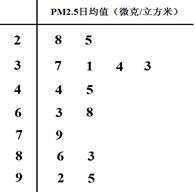
(1)从这15天的PM2.5日均监测数据中,随机抽出三天,求恰有一天空气质量达到一级的概率;
(2)从这15天的数据中任取三天数据,记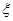 表示抽到PM2.5监测数据超标的天数,求
表示抽到PM2.5监测数据超标的天数,求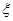 的分布列;
的分布列;
(3)以这15天的PM2.5日均值来估计一年的空气质量情况,则一年(按360天计算)中平均有多少天的空气质量达到一级或二级。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学号召本校学生在本学期参加市创办卫生城的相关活动,学校团委对该校学生是否关心创卫活动用简单抽样方法调查了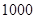 位学生(关心与不关心的各一半),
位学生(关心与不关心的各一半),
结果用二维等高条形图表示,如图.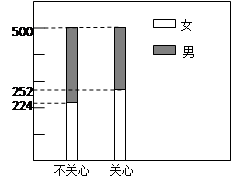
(1)完成列联表,并判断能否有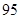 ℅的把握认为是否关心创卫活动与性别有关?
℅的把握认为是否关心创卫活动与性别有关?
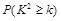 | 0.10 | 0.05 | 0.01 |
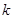 | 2.706 | 3.841 | 6.635 |
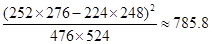
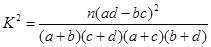 ;
;| | 女 | 男 | 合计 |
| 关心 | | | 500 |
| 不关心 | | | 500 |
| 合计 | | 524 | 1000 |
| 参加活动次数 | 1 | 2 | 3 |
| 人数 | 10 | 50 | 40 |
 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望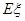 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com