
某中学号召本校学生在本学期参加市创办卫生城的相关活动,学校团委对该校学生是否关心创卫活动用简单抽样方法调查了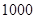 位学生(关心与不关心的各一半),
位学生(关心与不关心的各一半),
结果用二维等高条形图表示,如图.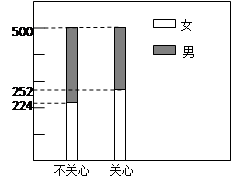
(1)完成列联表,并判断能否有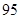 ℅的把握认为是否关心创卫活动与性别有关?
℅的把握认为是否关心创卫活动与性别有关?
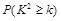 | 0.10 | 0.05 | 0.01 |
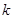 | 2.706 | 3.841 | 6.635 |
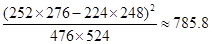
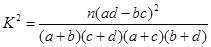 ;
;| | 女 | 男 | 合计 |
| 关心 | | | 500 |
| 不关心 | | | 500 |
| 合计 | | 524 | 1000 |
| 参加活动次数 | 1 | 2 | 3 |
| 人数 | 10 | 50 | 40 |
 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望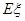 .
. (1)不能有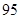 ℅的把握认为是否关心创卫活动与性别有关.
℅的把握认为是否关心创卫活动与性别有关.
(2)(i)他们参加活动次数恰好相等的概率为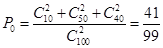
(ii) 分布列为
数学期望:
0 1 2 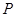
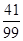


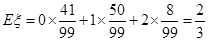 。
。
解析试题分析:(1)作出列联表:
科目:高中数学
来源:
题型:解答题
(本小题满分12分)
科目:高中数学
来源:
题型:解答题
第
科目:高中数学
来源:
题型:解答题
一般来说,一个人脚掌越长,他的身高就越高。现对10名成年人的脚掌长
科目:高中数学
来源:
题型:解答题
在一段时间内,某种商品价格
科目:高中数学
来源:
题型:解答题
某种产品的广告费支出
科目:高中数学
来源:
题型:解答题
有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下
科目:高中数学
来源:
题型:解答题
某校为了解高二学生
科目:高中数学
来源:
题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
由公式得 女 男 合计 关心 252 248 500 不关心 224 276 500 合计 476 524 1000 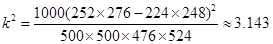
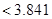 4分
4分
所以不能有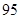 ℅的把握认为是否关心创卫活动与性别有关. 5分
℅的把握认为是否关心创卫活动与性别有关. 5分
(2)(i)他们参加活动次数恰好相等的概率为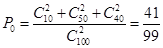 7分
7分
(ii) 从志愿者中任选两名学生,记“这两人中一人参加1次活动,另一个参加两次活动”为事件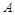 ,“这两人中一人参加2次活动,另一个参加3次活动”为事件
,“这两人中一人参加2次活动,另一个参加3次活动”为事件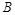 ,“这两人中一人参加1次活动,另一个参加两次活动”, “这两人中一人参加1次活动,另一个参加3次活动”为事件
,“这两人中一人参加1次活动,另一个参加两次活动”, “这两人中一人参加1次活动,另一个参加3次活动”为事件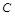 . 8分
. 8分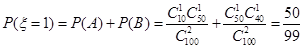 9分
9分 10分
10分
分布列为
0 1 2 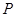


新课标综合测试卷系列答案
新课标青海中考系列答案
节节高大象出版社系列答案
新课标互动同步训练系列答案
新课标互动同步系列答案
中考冲刺60天系列答案
新疆中考总复习系列答案
新疆名师名校名卷系列答案
新疆名校中考模拟试卷系列答案
新疆新中考系列答案
某学校高二年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
(1)完成下面的 列联表;
列联表;
(2)在喜欢运动的女生中调查她们的运动时间, 发现她们的运动时间介于30分钟到90分钟之间,如图是测量结果的频率分布直方图,若从区间段
不喜欢运动
喜欢运动
合计
女生
50
男生
合计
100
200
 和
和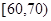 的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.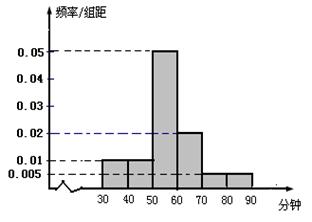
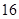 届亚运会于
届亚运会于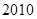 年
年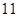 月
月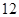 日至
日至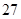 日在中国广州进行,为了做好接待工作,组委会招募了
日在中国广州进行,为了做好接待工作,组委会招募了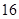 名男志愿者和
名男志愿者和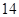 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有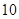 人和
人和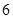 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱.
根据以上数据完成以下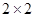 列联表:
列联表:
(2)能否在犯错误的概率不超过 喜爱运动 不喜爱运动 总计 男 10 16 女 6 14 总计 30 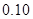 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志愿者中(其中恰有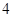 人会外语),抽取
人会外语),抽取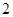 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中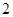 人都能胜任翻译工作的概率是多少?
人都能胜任翻译工作的概率是多少?
附:K2=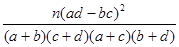
P(K2≥k) 0.100 0.050 0.025 0.010 0.001 k 2.706 3.841 5.024 6.635 10.828  与身高
与身高 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为 )作为样本如下表所示.
)作为样本如下表所示.
(1)在上表数据中,以“脚掌长”为横坐标,“身高”为纵坐标,作出散点图后,发现散点在一条直线附近,试求“身高”与“脚掌长”之间的线性回归方程 ;
;
(2)若某人的脚掌长为 ,试估计此人的身高;
,试估计此人的身高;
(3)在样本中,从身高180cm以上的4人中随机抽取2人作进一步的分析,求所抽取的2人中至少有1人身高在190cm以上的概率.
(参考数据: ,
, ,
, ,
, )
) (万元)和需求量
(万元)和需求量 之间的一组数据为:
之间的一组数据为:
(1)进行相关性检验;价 格 
1.4
1.6
1.8
2
2.2
需求量 
12
10
7
5
3
(2)如果 与
与 之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01
之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01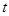 )
)
参考公式及数据: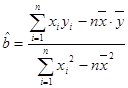 ,
,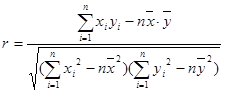 ,
,
相关性检验的临界值表:n-2
1
2
3
4
5
6
7
8
9
10
小概率0.01
1.000
0.990
0.959
0.917
0.874
0.834
0.798
0.765
0.735
0.708
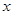 与销售额
与销售额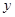 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
其中 x
2
4
5
6
8
y
30
40
60
50
70

(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告支出为10百万元时,销售额多大?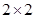 联表:
联表:
已知全部200人中随机抽取1人为优秀的概率为
优秀
非优秀
合计
甲班
30
乙班
50
合计
200
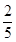
(1)请完成上面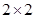 联表;
联表;
(2)根据列联表的数据,能否有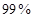 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系”
(3)从全部200人中有放回抽取3次,每次抽取一人,记被抽取的3人中优秀的人数为 ,若每次抽取得结果是相互独立的,求
,若每次抽取得结果是相互独立的,求 的分布列,期望
的分布列,期望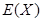 和方差
和方差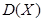
参考公式与参考数据如下:
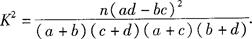
 、
、 两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试
两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试 、
、 两个学科的合格人数与不合格人数,得到以下2
两个学科的合格人数与不合格人数,得到以下2 2列联表:
2列联表:
(1)据此表格资料,你认为有多大把握认为“
 学科合格人数
学科合格人数
 学科不合格人数
学科不合格人数
合计
 学科合格人数
学科合格人数
40
20
60
 学科不合格人数
学科不合格人数
20
30
50
合计
60
50
110
 学科合格”与“
学科合格”与“ 学科合格”有关;
学科合格”有关;
(2)从“ 学科合格”的学生中任意抽取2人,记被抽取的2名学生中“
学科合格”的学生中任意抽取2人,记被抽取的2名学生中“ 学科合格”的人数为
学科合格”的人数为 ,求
,求 的数学期望.
的数学期望.
附公式与表:

0.15
0.10
0.05
0.025
0.010
0.005

2.072
2.706
3.841
5.024
6.635
7.879
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.
(1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个至多一个“成绩优秀”的概率;
(2)由以上统计数据填写下面列联表,并判断是否有90%的把握认为:“成绩优秀”与教学方式有关.
附:
甲班
(A方式)
乙班
(B方式)
总计
成绩优秀
成绩不优秀
总计


0.25
0.15
0.10
0.05
0.025
k
1.323
2.072
2. 706
3. 841
5. 024
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号