
某小区在一次对20岁以上居民节能意识的问卷调查中,随机抽取了100份问卷进行统计,得到相关的数据如下表: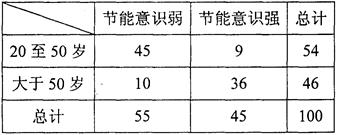
(Ⅰ)由表中数据直观分析,节能意识强弱是否与人的年龄有关?
(Ⅱ)据了解到,全小区节能意识强的人共有350人,估计这350人中,年龄大于50岁的有多少人?
(Ⅲ)按年龄分层抽样,从节能意识强的居民中抽5人,再从这5人中任取2人,求恰有1人年龄在20至50岁的概率.
(Ⅰ)节能意识强弱与年龄有关;(Ⅱ)年龄大于50岁的有280人;(Ⅲ)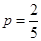 .
.
解析试题分析:(Ⅰ)因为20至50岁的54人有9人节能意识强,大于50岁的46人有36人节能意识强,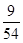 与
与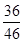 相差较大,所以节能意识强弱与年龄有关;(Ⅱ)根据比例即可求得年龄大于50岁的人数;(Ⅲ)分层抽样就是按比例抽样,根据比例可求得,年龄在20至50岁的抽1人,年龄大于50岁的抽4人,记这5人分别为A,B1,B2,B3,B4,从这5人中任取2人,将其结果一一列举出来,共有10种不同的结果,数出其中“恰有1人年龄在20至50岁”的基本事件的个数,即可得所求概率.
相差较大,所以节能意识强弱与年龄有关;(Ⅱ)根据比例即可求得年龄大于50岁的人数;(Ⅲ)分层抽样就是按比例抽样,根据比例可求得,年龄在20至50岁的抽1人,年龄大于50岁的抽4人,记这5人分别为A,B1,B2,B3,B4,从这5人中任取2人,将其结果一一列举出来,共有10种不同的结果,数出其中“恰有1人年龄在20至50岁”的基本事件的个数,即可得所求概率.
试题解析:(Ⅰ)因为20至50岁的54人有9人节能意识强,大于50岁的46人有36人节能意识强,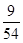 与
与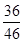 相差较大 1分,所以节能意识强弱与年龄有关 2分
相差较大 1分,所以节能意识强弱与年龄有关 2分
(Ⅱ)年龄大于50岁的有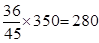 (人) 5分(列式2分,结果1分)
(人) 5分(列式2分,结果1分)
(Ⅲ)抽取节能意识强的5人中,年龄在20至50岁的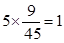 (人) 8分,
(人) 8分,
年龄大于50岁的4人 8分,记这5人分别为A,B1,B2,B3,B4。
从这5人中任取2人,共有10种不同取法 9分
完全正确列举 10分
设A表示随机事件“这5人中任取2人,恰有1人年龄在20至50岁”,则A中的基本事件有4种:完全正确列举 11分
故所求概率为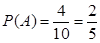 12分
12分
考点:1、统计基础知识;2、古典概型.


科目:高中数学 来源: 题型:解答题
某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组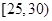 ,第2组
,第2组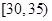 ,第3组
,第3组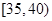 ,第4组
,第4组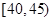 ,第5组
,第5组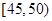 ,得到的频率分布直方图如图所示,下表是年龄的频率分布表.
,得到的频率分布直方图如图所示,下表是年龄的频率分布表.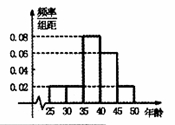

(1)求正整数 的值;
的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对某电子元件进行寿命追踪调查,所得情况如下频率分布直方图.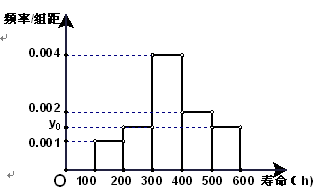
(1)图中纵坐标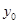 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原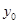 ;
;
(2)根据图表的数据按分层抽样,抽取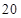 个元件,寿命为
个元件,寿命为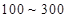 之间的应抽取几个;
之间的应抽取几个;
(3)从(2)中抽出的寿命落在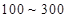 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为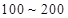 ,一个寿命为
,一个寿命为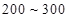 ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在2012年“双节”期间,高速公路车辆较多。某调查公司在一服务区从七座以下小型汽车中,按进服务区的先后每间隔50辆就抽取一辆的抽样方法,抽取了40名驾驶员进行调查,将他们在某段高速公路上的车速(km/t)分成6段: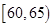 ,
, ,
, ,
, ,
, ,
, 后得到如图的频率分布直方图。问:
后得到如图的频率分布直方图。问:
(1)该公司在调查取样中,用到的是什么抽样方法?
(2)求这40辆小型汽车车速的众数和中位数的估计值;
(3)若从车速在 中的车辆中任取2辆,求抽出的2辆中速度在
中的车辆中任取2辆,求抽出的2辆中速度在 中的车辆数
中的车辆数 的分布列及其数学期望。(12分)
的分布列及其数学期望。(12分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图所示).已知图中从左到右的前3个小组的频率之比为1∶2∶3,第2小组的频数为12,求抽取的学生人数.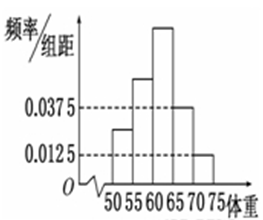
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组 ,第2组
,第2组 ,第3组
,第3组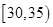 ,第4组
,第4组 ,第5组
,第5组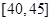 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.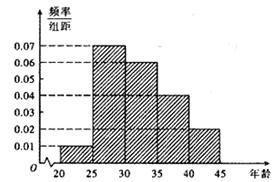
(Ⅰ)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(Ⅱ)在(1)的条件下,该市决定在第3,4组的志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人. 
(Ⅰ) 请估计一下这组数据的平均数M;
(Ⅱ) 现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
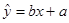 ;
;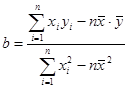 ,
, )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某学校高二年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
(1)完成下面的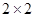 列联表;
列联表;
| | 不喜欢运动 | 喜欢运动 | 合计 |
| 女生 | 50 | | |
| 男生 | | | |
| 合计 | | 100 | 200 |
 和
和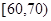 的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.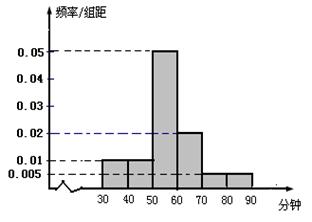
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com