
【题目】某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
组别 | 频数 | 频率 |
145.5~149.5 | 8 | 0.16 |
149.5~153.5 | 6 | 0.12 |
153.5~157.5 | 14 | 0.28 |
157.5~161.5 | 10 | 0.20 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 |
|
|
合计 |
|
|
(1)求出表中字母![]() 所对应的数值;
所对应的数值;
(2)在给出的直角坐标系中画出频率分布直方图;
(3)估计该校高一女生身高在149.5~165.5![]() 范围内有多少人?
范围内有多少人?
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点,焦点在![]() 轴上的椭圆,离心率为
轴上的椭圆,离心率为![]() 且过点
且过点![]() ,过定点
,过定点![]() 的动直线与该椭圆相交于
的动直线与该椭圆相交于![]() 、
、![]() 两点.
两点.
(1)若线段![]() 中点的横坐标是
中点的横坐标是![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为常数?若存在,求出点
为常数?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是圆
是圆![]() 上任意一点(
上任意一点(![]() 是圆心),点
是圆心),点![]() 与点
与点![]() 关于原点对称.线段
关于原点对称.线段![]() 的中垂线
的中垂线![]() 分别与
分别与![]() 交于
交于![]() 两点.
两点.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线经过![]() ,与抛物线
,与抛物线![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点.当以
两点.当以![]() 为直径的圆经过
为直径的圆经过![]() 时,求
时,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
将圆![]() 上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线
上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线![]() .
.
(1)写出曲线![]() 的参数方程;
的参数方程;
(2)以坐标原点为极点, ![]() 轴正半轴为极轴坐标建立极坐标系,已知直线
轴正半轴为极轴坐标建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别为曲线
分别为曲线![]() 和直线
和直线![]() 上的一点,求
上的一点,求![]() 的最近距离.
的最近距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
将圆![]() 上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线
上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线![]() .
.
(1)写出曲线![]() 的参数方程;
的参数方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴坐标建立极坐标系,已知直线
轴正半轴为极轴坐标建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别为曲线
分别为曲线![]() 和直线
和直线![]() 上的一点,求
上的一点,求![]() 的最近距离.
的最近距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分,规定满意度不低于98分,则评价该教师为“优秀”,现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶);
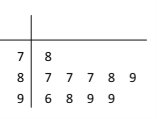
(1)指出这组数据的众数和中位数;
(2)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
(3)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,记![]() 表示抽到评价该教师为“优秀”的人数,求
表示抽到评价该教师为“优秀”的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地为弘扬中国传统文化举办“传统文化常识问答活动”,随机对该市![]() 岁的人群抽取一个容量为
岁的人群抽取一个容量为![]() 的样本,并将样本数据分成五组:
的样本,并将样本数据分成五组: ![]() ,再将其按从左到右的顺序分别编号为第
,再将其按从左到右的顺序分别编号为第![]() 组,第
组,第![]() 组,…,第
组,…,第![]() 组,绘制了样本的频率分布直方图,并对回答问题情况进行统计后,结果如下表所示.
组,绘制了样本的频率分布直方图,并对回答问题情况进行统计后,结果如下表所示.
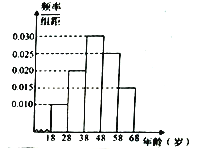
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第 | |
|
|
第 | |
|
|
第 | |
|
|
第 | |
|
|
第 | |
|
|
⑴分别求出![]() ,
, ![]() 的值;
的值;
⑵从![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,则第
人,则第![]() 组每组应各抽取多少人?
组每组应各抽取多少人?
⑶在⑵的前提下,决定在所抽取的![]() 人中随机抽取
人中随机抽取![]() 人颁发幸运奖,求所抽取的人中第
人颁发幸运奖,求所抽取的人中第![]() 组至少有
组至少有![]() 人获得幸运奖的概率.
人获得幸运奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com