
已知 按下列条件求
按下列条件求 值。
值。
(1) ; (2)
; (2)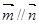 .
.
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
 已知椭圆E:
已知椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
已知a=(4,3),b=(-1,2),m=a-λb,n=2a+b,按下列条件求λ的值.
(1)m⊥n ;(2)m∥n;(3)m与n的夹角为钝角.
查看答案和解析>>
科目:高中数学 来源:2010年河南师大附中高考数学模拟试卷(理科)(解析版) 题型:解答题
 (a>b>0)的离心率
(a>b>0)的离心率 ,在椭圆E上存在A,B两点关于直线l:y=x+1对称.
,在椭圆E上存在A,B两点关于直线l:y=x+1对称. ;③椭圆E的左、右焦点到直线l的距离之比为
;③椭圆E的左、右焦点到直线l的距离之比为 .
.
查看答案和解析>>
科目:高中数学 来源:2010年河南师大附中高三5月考前预测数学试卷(理科)(解析版) 题型:解答题
 (a>b>0)的离心率
(a>b>0)的离心率 ,在椭圆E上存在A,B两点关于直线l:y=x+1对称.
,在椭圆E上存在A,B两点关于直线l:y=x+1对称. ;③椭圆E的左、右焦点到直线l的距离之比为
;③椭圆E的左、右焦点到直线l的距离之比为 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com