Question

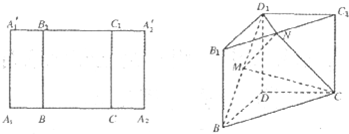
如图，矩形A₁A₂A′₂A′₁，满足B、C在A₁A₂上，B₁、C₁在A′₁A′₂上，且BB₁∥CC₁∥A₁A′₁，A₁B=CA₂=2，BC=2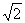，A₁A′₁=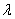，沿BB₁、CC₁将矩形A₁A₂A′₂A′₁折起成为一个直三棱柱，使A₁与A₂、A′₁与A′₂重合后分别记为D、D₁，在直三棱柱DBC-D₁B₁C₁中，点M、N分别为D₁B和B₁C₁的中点．

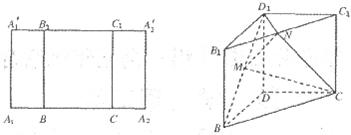
(I)证明：MN∥平面DD₁C₁C；

(Ⅱ)若二面角D_1-MN-C为直二面角，求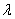的值．

 

Answer 1

【答案】

（1）要证明线面平行，只要通过线线平行来加以证明即可。

（2）

【解析】

试题分析：解：（Ⅰ）证：连结DB₁ 、DC₁ ∵四边形DBB₁D₁为矩形，M为D₁B的中点   2分

∴M是DB₁与D₁B的交点，且M为DB₁的中点

∴MN∥DC₁，∴MN∥平面DD₁C₁C                              4分

（Ⅱ）解：四边形为矩形，B.C在A₁A₂上，B₁.C₁在上，

且BB₁∥CC₁∥，A₁B = CA₂ = 2，，

∴∠BDC = 90°                                            6分

以DB、DC、DD₁所在直线分别为x.y.z轴建立直角坐标系，则

D(0，0，0)，B(2，0，0)，C(0，2，0)，D₁(0，0，)，B₁(2，0，)，C₁(0，2，)

点M、N分别为D₁B和B₁C₁的中点，∴

设平面D₁MN的法向量为m = (x，y，z)，则

，

令x = 1得：

即                                             8分

设平面MNC的法向量为n = (x，y，z)，则

，令z = 1得：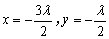

即                                         10分

∵二面角D₁－MN－C为直二面角    ∴m⊥n，故，解得：

∴二面角D₁－MN－C为直二面角时，．         12分

考点：线面平行，二面角的平面角

点评：解决的关键是根据已知条件熟练的根据判定定理证明，同时，建立空间直角坐标系，然后借助于向量的知识来得到二面角的平面角的表示，属于基础题。