
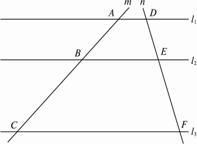
图1-1-23
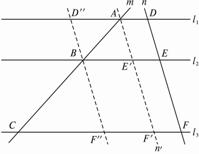
图1-1-24
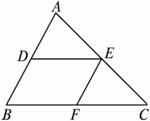
图1-1-25
(1)分别量出线段AB、AC、DE、DF的长,观察结论,你有什么发现?
(2)把直线n沿DA方向平移到A点,得到直线n′,分别与直线l2、l3交于E′、F′,如图1-1-24,观察△ABE′与△ACF′,你有什么发现?说出你的猜测,并验证.
(3)如图1-1-24,若继续把直线n平移使其经过B点,分别与直线l1、l3交于D″、F″,结果如何??
(4)利用你的发现,判断图1-1-25中的相似三角形有几对?
思路分析:对于线段的关系,尤其是四条线段的关系,很有可能是成比例,但要通过验证才能确定.而两个三角形在大小不一的情况下,又有了成比例的线段,就可以联想到两个三角形相似.要判断最后一个图形中有几对相似三角形,就要设法把图形分离出(2)(3)中的基本图形.
解:(1)通过测量可得AB =1.5 cm,AC =4 cm,DE =1.15cm,DF =3.1 cm,观察且计算可发现![]() =
=![]() =0.375,
=0.375,![]() =
=![]() ≈0.371,由于作图和测量都会有一定的误差,因此可以确定有
≈0.371,由于作图和测量都会有一定的误差,因此可以确定有![]() =
=![]() .?
.?
(2)△ABE′∽△ACF′,由于AF′是由DF平移而来的,由平移的特征可得AE′=DE,AF′=DF,所以仍然有![]() =
=![]() =
=![]() .而通过测量同样可计算出
.而通过测量同样可计算出![]() 的值也非常接0.375,因此有
的值也非常接0.375,因此有![]() =
=![]() =
=![]() ;由平行线的性质,可得∠ABE =∠ACF,∠AE′B =AF′C.而∠CAF′为公共角.
;由平行线的性质,可得∠ABE =∠ACF,∠AE′B =AF′C.而∠CAF′为公共角.
所以△ABE′∽△ACF′.?
(3)△ABD″∽△CBF″.?
(4)有3对:△ADE∽△ABC,△CEF∽△CAB,△ADE∽△EFC.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图示,已知直线l1∥l2,点A是l1,l2之间的一个定点,且A到l1,l2的距离分别为4、3,点B是直线l1上的动点,若
如图示,已知直线l1∥l2,点A是l1,l2之间的一个定点,且A到l1,l2的距离分别为4、3,点B是直线l1上的动点,若| AC |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
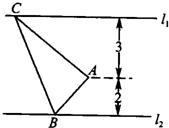 如图,已知直线l1∥l2,点A是l1,l2之间的定点,点A到l1,l2之间的距离分别为3和2,点B是l2上的一动点,作AC⊥AB,且AC与l1交于点C,则△ABC的面积的最小值为
如图,已知直线l1∥l2,点A是l1,l2之间的定点,点A到l1,l2之间的距离分别为3和2,点B是l2上的一动点,作AC⊥AB,且AC与l1交于点C,则△ABC的面积的最小值为查看答案和解析>>
科目:高中数学 来源: 题型:
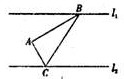 如图,已知直线l1∥l2,点A是l1,l2上两直线之间的动点,且到l1距离为4,到l2距离为3,若
如图,已知直线l1∥l2,点A是l1,l2上两直线之间的动点,且到l1距离为4,到l2距离为3,若| AC |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
A.若l1![]() α,l2∩α=A,则l1,l2为异面直线
α,l2∩α=A,则l1,l2为异面直线
B.若l1∥l2,l1∥α,则l2∥α
C.若l1⊥l2,l1⊥α,则l2∥α
D.若l1⊥α,l2⊥α,则l1∥l2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com