
| 1 |
| x |
| 1 | ||
|
| 1 |
| 2 |
| 1 | ||
|
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 | ||
|
| 1 | ||
|
|
| 1 |
| x |
| 1 |
| x |
| 1 | ||
|
| 1 |
| x |
| ||
|
| 1 |
| x |
| ||
|
| 1 |
| x |
| x | ||||
|
| 1 | ||
1+x+
|
| 1 |
| x |
| 1 |
| 2 |
| 1 | ||
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 | ||
|
| 1 |
| 2 |
| 1 | ||
2
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 | ||
|
| 1 | ||
|
|
| ||||
|
| |x1-x2| | ||||||||
|
| 1+x2 |
| 1+x1 |
| 1+x1 |
| 1+x2 |
| 1 |
| 2 |
| 1 | ||
|
|
| 1 |
| x |
| ||
| 2 |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |


 УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
| 1 |
| x |
| 1 | ||
|
| 1 |
| 2 |
| 1 | ||
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК2010ФъНЫеЪЁбяжнЪаЦкФЉЪ§бЇИДЯАЪдОэ3ЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
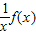 ЮЊМѕКЏЪ§ЃЌдђГЦКЏЪ§fЃЈxЃЉЮЊЁАШѕдіЁБКЏЪ§ЃЎвбжЊКЏЪ§
ЮЊМѕКЏЪ§ЃЌдђГЦКЏЪ§fЃЈxЃЉЮЊЁАШѕдіЁБКЏЪ§ЃЎвбжЊКЏЪ§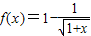 ЃЎ
ЃЎ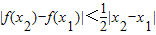 ЃЛ
ЃЛ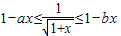 КуГЩСЂЃЌЧѓЪЕЪ§aЃЌbЕФШЁжЕЗЖЮЇЃЎ
КуГЩСЂЃЌЧѓЪЕЪ§aЃЌbЕФШЁжЕЗЖЮЇЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃКЙуЖЋШ§ФЃ ЬтаЭЃКНтД№Ьт
| 1 |
| x |
| 1 | ||
|
| 1 |
| 2 |
| 1 | ||
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК2011ФъНЫеЪЁФЯОЉЪаН№СъжабЇИпПМЪ§бЇдЄВтЪдОэЃЈ1ЃЉЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
 ЮЊМѕКЏЪ§ЃЌдђГЦКЏЪ§fЃЈxЃЉЮЊЁАШѕдіКЏЪ§ЁБЃЎвбжЊКЏЪ§fЃЈxЃЉ=1-
ЮЊМѕКЏЪ§ЃЌдђГЦКЏЪ§fЃЈxЃЉЮЊЁАШѕдіКЏЪ§ЁБЃЎвбжЊКЏЪ§fЃЈxЃЉ=1-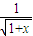 ЃЎ
ЃЎ ЃЛ
ЃЛ Ём1-bxКуГЩСЂЃЌЧѓЪЕЪ§aЃЌbЕФШЁжЕЗЖЮЇЃЎ
Ём1-bxКуГЩСЂЃЌЧѓЪЕЪ§aЃЌbЕФШЁжЕЗЖЮЇЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com