
分析 由新定义,利用导数逐一求出函数y=x3、y=x2+1在点A与点B之间的“弯曲度”判断①、③;举例说明②正确;求出曲线y=ex上不同两点A(x1,y1),B(x2,y2)之间的“弯曲度”,然后结合不等式的性质,即可判断④.
解答 解:对于①,由y=x3,得y′=3x2,
则kA=3,kB=3,则|kA-kB|=0,则φ(A,B)=0,故①正确;
对于②,如y=1时,y′=0,则φ(A,B)=0,故②正确;
对于③,抛物线y=x2+1的导数为y′=2x,yA=xA2+1,yB=xB2+1,
yA-yB=xA2-xB2=(xA-xB)(xA+xB),
则φ(A,B)=$\frac{{|{k_A}-{k_B}|}}{|AB|}$=$\frac{|2{x}_{A}-2{x}_{B}|}{\sqrt{({x}_{A}-{x}_{B})^{2}+({y}_{A}-{y}_{B})^{2}}}$=$\frac{2}{\sqrt{1+({x}_{A}+{x}_{B})^{2}}}$≤2,故③正确;
对于④,由y=ex,得y′=ex,φ(A,B)=$\frac{|{e}^{{x}_{1}}-{e}^{{x}_{2}}|}{\sqrt{({x}_{1}-{x}_{2})^{2}+({e}^{{x}_{1}}-{e}^{{x}_{2}})^{2}}}$,
由不同两点A(x1,y1),B(x2,y2),可得φ(A,B)<$\frac{|{e}^{{x}_{1}}-{e}^{{x}_{2}}|}{\sqrt{0+({e}^{{x}_{1}}-{e}^{{x}_{2}})^{2}}}$=1,
故④正确.
故答案为:①②③④
点评 本题是新定义题,考查了命题的真假判断与应用,考查了利用导数研究过曲线上某点的切线方程,考查了函数恒成立问题,关键是对题意的理解.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
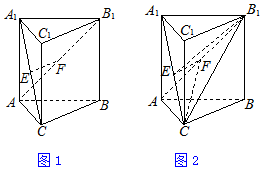 如图,三棱柱ABC-A1B1C1中,侧棱AA1与底面垂直,∠ACB=90°,AC=BC,AA1=AB=2,E,F分别是A1C,AB1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1与底面垂直,∠ACB=90°,AC=BC,AA1=AB=2,E,F分别是A1C,AB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
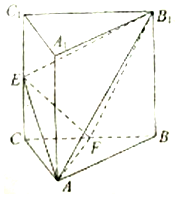 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,E,F分别是CC1,BC的中点,且AB=AA1.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,E,F分别是CC1,BC的中点,且AB=AA1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com