
如图,在直角梯形ABEF中,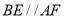 ,
,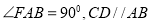 ,讲DCEF沿CD折起,使得
,讲DCEF沿CD折起,使得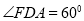 ,得到一个几何体,
,得到一个几何体,

(1)求证: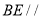 平面ADF;
平面ADF;
(2)求证:AF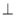 平面ABCD;
平面ABCD;
(3)求三棱锥E-BCD的体积.
(1)见解析(2)见解析(3)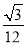
【解析】
试题分析:
(1)要证明 平面ADF,可以通过BCE面与ADF面平行来得到线面平行,在折叠过程中,会保持BC//AD,CE//DF,故两平面内两条相交的直线相互平行,故可以证明BCE面与ADF面平行来得到线面平行
平面ADF,可以通过BCE面与ADF面平行来得到线面平行,在折叠过程中,会保持BC//AD,CE//DF,故两平面内两条相交的直线相互平行,故可以证明BCE面与ADF面平行来得到线面平行
(2)要证明AF垂直于ABCD面,只需要证明AF与ABCD面内两条相交的直线AD与DC垂直即可,利用三角形ADF的正弦定理,可以求出AF长度,加以勾股定理就可以证明AF与AD垂直,DC垂直于DF和AD,所以DC垂直于面AFD,进而也是垂直于AF的.
(3)求三棱锥E-BCD的体积,由(1)(2)可以知道面BCE与面ADF平行且DC垂直于面ADF,进而有DC垂直于面BCE,所以求三棱锥的体积可以以三角形BCE底面,DC为高,则高长度已知,底面三角形面积可以利用EC,BC及其两边夹角的正弦值来求的.
试题解析:
(1)由已知条件可知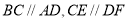 ,折叠之后平行关系不变,又因为
,折叠之后平行关系不变,又因为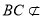 平面
平面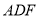 ,
,
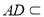 平面
平面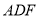 ,所以
,所以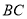 //平面
//平面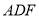 ;
;
同理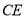 //平面
//平面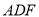 . 2分
. 2分
又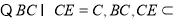 平面
平面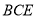 ,
,
 平面
平面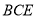 //平面
//平面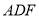 .
.
又 平面
平面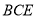 ,
,
∴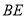 //平面
//平面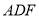 . 4分
. 4分
(2)由于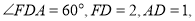
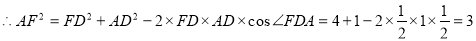 ,即
,即
 . 6分
. 6分
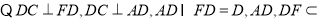 平面
平面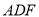 ,
,
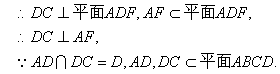
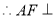 平面
平面 . 8分
. 8分
(3)法一: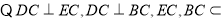 平面
平面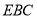 ,
,
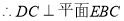 . 10分
. 10分
又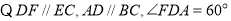 ,
, .
.

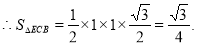 12分
12分
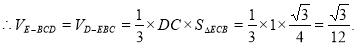 14分
14分
法二:取 中点
中点 ,连接
,连接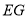 .
.
由(2)易知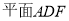 ⊥平面
⊥平面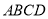 ,又平面
,又平面 //平面
//平面 ,
,

 ⊥平面
⊥平面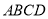 . 10分
. 10分
又 ,
, .
.

 ,
,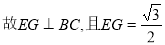 , 12分
, 12分
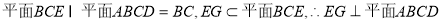 .
.
 . 14分
. 14分
考点:线面平行面面平行线面垂直三棱锥体积


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源:2013-2014学年广东省湛江市高三高考模拟测试二理科数学试卷(解析版) 题型:选择题
下列命题正确的是( )
A.若两条直线和同一个平面所成的角相等,则这两条直线平行
B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行
C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行
D.若两个平面都垂直于第三个平面,则这两个平面平行
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省梅州市高三3月总复习质检理科数学试卷(解析版) 题型:选择题
在复平面内,复数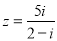 的对应点位于( )
的对应点位于( )
A.第一象限 B.第二象限 C.第三象限角 D.第四象限
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省梅州市高三3月总复习质检文科数学试卷(解析版) 题型:填空题
已知双曲线C的焦点、实轴端点恰好是椭圆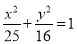 的长轴的端点、焦点,则双曲线C的方程为_______.
的长轴的端点、焦点,则双曲线C的方程为_______.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省梅州市高三3月总复习质检文科数学试卷(解析版) 题型:选择题
已知某几何体的三视图如图所示,则该几何体的体积是( )
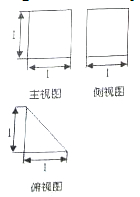
A.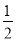 B.
B.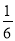 C.
C. D.
D.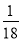
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com