
(本题满分14分)
某学校拟建一座长![]() 米,宽
米,宽![]() 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔![]() 米需打建一个桩位,每个桩位需花费
米需打建一个桩位,每个桩位需花费![]() 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的![]() 米墙面需花
米墙面需花![]() 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当![]() 为何值时,所需总费用最少?
为何值时,所需总费用最少?
每隔3米打建一个桩位时,所需总费用最小为1170万元.
由题意可知,需打![]() 个桩位. …………3分
个桩位. …………3分
墙面所需费用为:![]() , ………………ks5u
, ………………ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
5分
∴所需总费用![]()
![]() (
(![]() ) ………9分
) ………9分
令![]() ,则
,则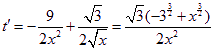 ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .∴当
.∴当![]() 时,
时,![]() 取极小值为
取极小值为![]() .
.
而在![]() 内极值点唯一,所以
内极值点唯一,所以![]() .∴当
.∴当![]() 时,
时,![]() (万元),
(万元),
即每隔3米打建一个桩位时,所需总费用最小为1170万元. ………ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
…ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
14分


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
| π |
| 3 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,![]() 为
为![]() 上的点,且BF⊥平面ACE.
上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;(2)求三棱锥D-AEC的体积;(3)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三上学期期中考试数学 题型:解答题
(本题满分14分)已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}
(Ⅰ)若A B=[0,3],求实数m的值
B=[0,3],求实数m的值
(Ⅱ)若A CRB,求实数m的取值范围
CRB,求实数m的取值范围
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三上学期第三次月考理科数学卷 题型:解答题
(本题满分14分)
已知点 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 作
作 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。
(1)求动点 的轨迹方程;
的轨迹方程;
(2)已知点 ,在动点
,在动点 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2014届江西省高一第二学期入学考试数学 题型:解答题
(本题满分14分)已知函数 .
.
(1)求函数 的定义域;
的定义域;
(2)判断 的奇偶性;
的奇偶性;
(3)方程 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使

 ;如果没有,请说明理由?(注:区间的长度为
;如果没有,请说明理由?(注:区间的长度为 ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com