Question

3．观察下列等式

照此规律，第100个等式1²-2²+3²-4²+…-100²=-5050．

Answer 1

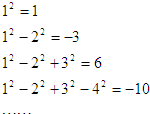
分析 观察可得：等式的左边是连续正整数的平方差相加的形式，根据这一规律得第100个等式左边为1²-2²+3²-4²+…+99²-100²，利用分组求和法、等差数列的前n项和公式求出左边式子的和．

解答 解：观察下列等式：
1²=1
1²-2²=-3
1²-2²+3²=6
1²-2²+3²-4²=-10 …
当n=100时，左边=（1²-2²）+（3²-4²）+…+[（99）²-100²]
=-（3+7+11+199）=-$\frac{50（3+199）}{2}$=-5050，
故答案为：-5050．

点评 本题考查了归纳推理，以及分组求和法、等差数列的前n项和公式的应用，归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．