Question

【题目】已知点A，B分别为椭圆E： 的左，右顶点，点P（0，﹣2），直线BP交E于点Q， 且△ABP是等腰直角三角形．
（Ⅰ）求椭圆E的方程；
（Ⅱ）设过点P的动直线l与E相交于M，N两点，当坐标原点O位于以MN为直径的圆外时，求直线l斜率的取值范围．

Answer 1

【答案】解：（Ⅰ）由题意知：△ABP是等腰直角三角形，a=2，B（2，0），

设Q（x0，y0），由 ，则 ，

代入椭圆方程，解得b2=1，

∴椭圆方程为 ．

（Ⅱ）由题意可知，直线l的斜率存在，方程为y=kx﹣2，设M（x1，y1），N（x2，y2），

则 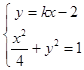，整理得：（1+4k2）x2﹣16kx+12=0，

由韦达定理可知：x1+x2= ，x1x2= ，

由直线l与E有两个不同的交点，则△＞0，

即（﹣16k）2﹣4×12×（1+4k2）＞0，解得：k2＞ ，…①

由坐标原点O位于以MN为直径的圆外，则 ，即x1x2+y1y2＞0，

则x1x2+y1y2=x1x2+（kx1﹣2）（kx2﹣2）

=（1+k2）x1x2﹣2k×（x1+x2）+4

=（1+k2） ﹣2k× +4＞0，

解得：k2＜4，…②

综合①②可知： ＜k2＜4，解得 ＜k＜2或﹣2＜k＜﹣ ，

直线l斜率的取值范围（﹣2，﹣ ）∪（ ，2）．

【解析】（Ⅰ）由题意可知：由 ，求得Q点坐标，即可求得椭圆E的方程；（Ⅱ）设直线y=kx﹣2，代入椭圆方程，由韦达定理，由△＞0，由坐标原点O位于以MN为直径的圆外，则 ，由向量数量积的坐标公式，即可求得直线l斜率的取值范围．