
已知![]() 是定义在R上的函数,其图象交x轴于A,B,C三点,若点B的坐标为(2,0),且
是定义在R上的函数,其图象交x轴于A,B,C三点,若点B的坐标为(2,0),且![]() 在
在![]() 和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(1)求c的值;
(2)在函数![]() 的图象上是否存在一点M(x0,y0),使得
的图象上是否存在一点M(x0,y0),使得![]() 在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,说明理由;
在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,说明理由;
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 3 |
| 2 |
| A、1 | B、-1 | C、2 | D、-2 |
查看答案和解析>>
科目:高中数学 来源:辽宁 题型:单选题
| A.0是f(x)的极大值,也是g(x)的极大值 |
| B.0是f(x)的极小值,也是g(x)的极小值 |
| C.0是f(x)的极大值,但不是g(x)的极值 |
| D.0是f(x)的极小值,但不是g(x)的极值 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省高三三月月考数学(理)试卷 题型:选择题
已知函数 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,在[0,2]上
,在[0,2]上 是增函
是增函
数,则下列结论:
(1)若 ,则
,则 ;[来源:Z§xx§k.Com]
;[来源:Z§xx§k.Com]
(2)若 且
且 ;
;
(3)若方程 在[-8,8]内恰有四个不同的根
在[-8,8]内恰有四个不同的根 ,则
,则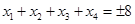 ;
;
其中正确的有( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com