
 的角A的取值范围.
的角A的取值范围. ,结合C为三角形的内角,即可得到角C的大小;
,结合C为三角形的内角,即可得到角C的大小; ,可得sin(A
,可得sin(A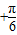 )≥
)≥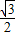 .再结合正弦函数的图象与性质,即可算出满足条件的角A的取值范围.
.再结合正弦函数的图象与性质,即可算出满足条件的角A的取值范围.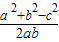 =
= ,
,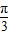 …(6分)
…(6分) 即sinA+sin(A+C)≥
即sinA+sin(A+C)≥ ,…(7分)
,…(7分) sinA+
sinA+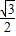 cosA≥
cosA≥ ,可得
,可得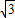 (sinAcos
(sinAcos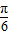 +cosAsin
+cosAsin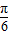 )≥
)≥ ,
,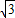 sin(A
sin(A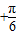 )
)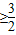 ,即sin(A
,即sin(A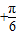 )≥
)≥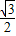 ,…(9分)
,…(9分)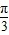 ≤A+
≤A+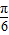 ≤
≤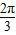 ,可得
,可得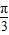 ≤A≤
≤A≤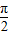 .…(12分)
.…(12分)

科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com