Question

【题目】如图，在四棱锥P﹣ABCD中，△PAD为正三角形，四边形ABCD为直角梯形，CD∥AB，BC⊥AB，平面PAD⊥平面ABCD，点E、F分别为AD、CP的中点，AD=AB=2CD=2．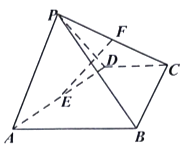
（Ⅰ）证明：直线EF∥平面PAB；
（Ⅱ）求直线EF与平面PBC所成角的正弦值．

Answer 1

【答案】证明：（Ⅰ）取BC中点M，连结EM，FM，

∵点E、F分别为AD、CP的中点，∴EM∥AB，FM∥PB，

∵EM平面PAB，AB平面PAB，∴EM∥平面PAB，

∵FM平面PAB，PB平面PAB，∴FM∥平面PAB，

∵EM∩FM=M，EM、FM平面PEM，

∵平面EFM∥平面PAB，

∵EF平面PEM，∴EF∥平面PAB．

（Ⅱ）解：连结PE、PM，

∵平面PAD⊥平面ABCD，∴PE⊥平面ABCD，PE⊥BC，

∵EM⊥BC，∴BC⊥平面PEM，

∵BC平面PBC，∴平面PBC⊥平面PEM，

过点E作EH⊥PM于点H，连结FH，

由平面PBC⊥平面PEM，得EH⊥平面PBC，

∴直线EF与平面PBC所成角为∠EFH，

在直角三角形PEC中，EF= PC= ，

在直角三角形PEM中，EH= ，

∴sin = = ．

∴直线EF与平面PBC所成角的正弦值为 ．

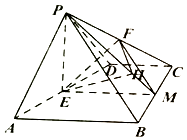
【解析】（Ⅰ）取BC中点M，连结EM，FM，推导出EM∥平面PAB，FM∥平面PAB，从而平面EFM∥平面PAB，由此能证明EF∥平面PAB．（Ⅱ）连结PE、PM，推导出PE⊥BC，EM⊥BC，从而BC⊥平面PEM，进而平面PBC⊥平面PEM，过点E作EH⊥PM于点H，连结FH，则EH⊥平面PBC，直线EF与平面PBC所成角为∠EFH，由此能求出直线EF与平面PBC所成角的正弦值．
【考点精析】本题主要考查了直线与平面平行的判定和空间角的异面直线所成的角的相关知识点，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则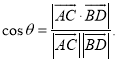才能正确解答此题．