
(![]() 分)如图,
分)如图,![]() 是曲线
是曲线
![]() 上的
上的![]() 个点,点
个点,点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() 是正三角形(
是正三角形(![]() 是坐标原点) .
是坐标原点) .
(Ⅰ) 写出![]() ;
;
(Ⅱ)求出点![]()
![]() 的横坐标
的横坐标![]() 关于
关于![]() 的表达式;
的表达式;
(Ⅲ)设![]() ,若对任意正整数
,若对任意正整数![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.

解析:(Ⅰ) ![]() .…………………………………………… 2分
.…………………………………………… 2分
(Ⅱ)依题意![]() ,则
,则
![]() ,
,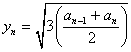 … 3分
… 3分
在正三角形![]() 中,有
中,有
![]() .
.
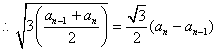 .…………………………………………………… 4分
.…………………………………………………… 4分
![]() ,
,
![]() , ①
, ①
同理可得![]() . ②
. ②
①-②并变形得
![]()
![]() ,
,
![]() , ………………………………… 6分
, ………………………………… 6分
![]() .
.
∴数列![]() 是以
是以![]() 为首项,公差为
为首项,公差为![]() 的等差数列.
的等差数列.
![]() , …………………………………… 7分
, …………………………………… 7分
![]()
![]() ,
,
![]()
![]() .
.
![]() . ………………………… 8分
. ………………………… 8分
(Ⅲ)解法1 :∵![]() ,
,
∴![]() .
.
![]()
![]()
![]() .
.
∴当![]() 时,上式恒为负值,
时,上式恒为负值,
∴当![]() 时,
时,![]() ,
,
∴数列![]() 是递减数列.
是递减数列.
![]() 的最大值为
的最大值为![]() . ………………………………………………… 11分
. ………………………………………………… 11分
若对任意正整数![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,则不等式
恒成立,则不等式![]() 在
在![]() 时恒成立,即不等式
时恒成立,即不等式![]() 在
在![]() 时恒成立.
时恒成立.
设![]() ,则
,则![]() 且
且![]() ,
,
∴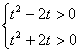
解之,得 ![]() 或
或![]() ,
,
即![]() 的取值范围是
的取值范围是![]() .…………………………………………… 14分
.…………………………………………… 14分


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源:2010-2011年江苏省如皋市五校高二下学期期中考试文科数学 题型:解答题
(本小题满分12分)
如图,点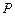 是椭圆
是椭圆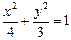 上一动点,点
上一动点,点 是点
是点 在
在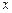 轴上的射影,坐标平面
轴上的射影,坐标平面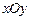 内动点
内动点 满足:
满足: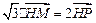 (
( 为坐标原点),设动点
为坐标原点),设动点 的轨迹为曲线
的轨迹为曲线 .
.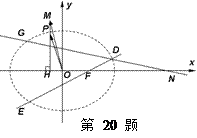
(Ⅰ)求曲线 的方程并画出草图;
的方程并画出草图;
(Ⅱ)过右焦点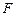 的直线
的直线 交曲线
交曲线 于
于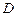 ,
,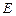 两点,且
两点,且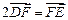 ,点
,点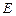 关于
关于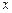 轴的对称点为
轴的对称点为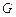 ,求直线
,求直线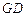 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2011届广东省高考猜押题卷文科数学(三)解析版 题型:解答题
(本题满分12分)
如图6,在平面直角坐标系 中,设点
中,设点 ,直线
,直线 :
: ,点
,点 在直线
在直线 上移动,
上移动, 是线段
是线段 与
与 轴的交点,
轴的交点,  .
.
(I)求动点 的轨迹的方程
的轨迹的方程 ;
;
(II)设圆 过
过 ,且圆心
,且圆心 在曲线
在曲线 上,
上, 是圆
是圆 在
在 轴上截得的弦,当
轴上截得的弦,当 运动时弦长
运动时弦长 是否为定值?请说明理由.
是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011届陕西省师大附中、西工大附中高三第七次联考理数 题型:填空题
选 做题(请考生在以下三个小题中任选一题做答,如果多做,则按所做的第一题评阅记分)
做题(请考生在以下三个小题中任选一题做答,如果多做,则按所做的第一题评阅记分)
A.(选修4—4坐标系与参数方程)已知点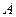 是
是 曲线
曲线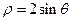 上任意一点,则点
上任意一点,则点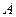 到直线
到直线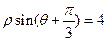 的距离的最小值是
的距离的最小值是  .
.
B.(选修4—5不等 式选讲)
式选讲) 不等式
不等式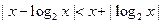 的解集是
的解集是  .
.
C.(选修4—1几何证明选讲)如图所示,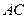 和
和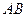 分别是圆
分别是圆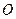 的切线,且
的切线,且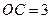 ,
, 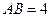 ,延长
,延长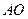 到
到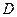 点,则
点,则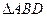 的面积是 .
的面积是 .
查看答案和解析>>
科目:高中数学 来源:2010-2011年江苏省如皋市五校高二下学期期中考试文科数学 题型:解答题
(本小题满分12分)
如图,点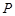 是椭圆
是椭圆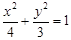 上一动点,点
上一动点,点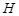 是点
是点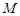 在
在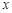 轴上的射影,坐标平面
轴上的射影,坐标平面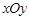 内动点
内动点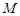 满足:
满足: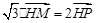 (
(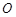 为坐标原点),设动点
为坐标原点),设动点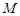 的轨迹为曲线
的轨迹为曲线 .
.
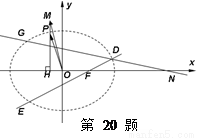
(Ⅰ)求曲线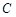 的方程并画出草图;
的方程并画出草图;
(Ⅱ)过右焦点 的直线
的直线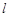 交曲线
交曲线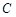 于
于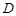 ,
,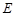 两点,且
两点,且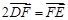 ,点
,点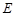 关于
关于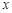 轴的对称点为
轴的对称点为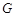 ,求直线
,求直线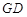 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com