
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 (1)根据终边相同的角的同名三角函数的值的定义进行判断,
(2)根据三角函数正弦函数的定义进行判断
(3)根据三角函数的定义进行判断
(4)根据三角函数的定义进行判断.
解答 解:(1)终边相同的角的同名三角函数的值相等,正确,
(2)若sinα>0,则α是第一、二象限的角或者在y轴的正半轴,故(2)错误,
(3)终边不同的角的同名三角函数的值不可能相等,错误,如sin$\frac{π}{6}$=sin$\frac{5π}{6}$=$\frac{1}{2}$,
(4)三角函数的值确定,则角的大小不确定,错误比如sinx=$\frac{1}{2}$,则x=$\frac{π}{6}$,x=$\frac{5π}{6}$都可以,
故(2)(3)(4)错误,
故选:C
点评 本题主要考查命题的真假判断,涉及三角函数的定义,角的取值和三角函数的符号,涉及的知识点较多,但难度不大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
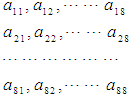 64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,每一列的数都成等比数列且每列数的公比都等于q,且a11=$\frac{1}{2}$,a24=1,a32=$\frac{1}{4}$.
64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,每一列的数都成等比数列且每列数的公比都等于q,且a11=$\frac{1}{2}$,a24=1,a32=$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{4}$,$\frac{π}{3}$) | B. | (0,$\frac{π}{3}$)∪($\frac{3π}{4}$,π) | C. | ($\frac{3π}{4}$,$\frac{5π}{6}$) | D. | ($\frac{2π}{3}$,$\frac{3π}{4}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com