
(1)当α=![]() ,且
,且![]() =(2,
=(2,![]() )时,求P点的坐标;
)时,求P点的坐标;
(2)当![]() ·
·![]() =0时,求|
=0时,求|![]() |的值;
|的值;
(3)求|AB|的最小值.
解:(1)设![]() =(x,y),则由
=(x,y),则由![]() ·
·![]() =0及点B在双曲线上,得
=0及点B在双曲线上,得

解得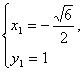 或
或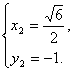
∴![]() =(-
=(-![]() ,1)或
,1)或![]() =(
=(![]() ,-1).
,-1).
∴![]() =
=![]()
![]() +
+![]()
![]() =(
=(![]() ,
,![]() )或
)或
![]() =
=![]()
![]() +
+![]()
![]() =(
=(![]() ,
,![]() ),
),
即P点的坐标是(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
(2)设直线OA的方程为y=kx,则由
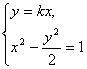 得x2=
得x2=![]() ,y2=
,y2=![]() .
.
∴|OA|2=x2+y2=![]() .
.
同理,可得|OB|2=![]() .
.
由|OP|·|AB|=|OA|·|OB|,得![]() =
=![]() =
=![]() +
+![]() =
=![]() .
.
∴|OP|=![]() .
.
(3)方法一:由|OP|·|AB|=|OA|·|OB|,![]() =
=![]() =
=![]() ,
,
(|OA|2+|OB|2)(![]() )≥4,
)≥4,
∴|AB|2≥8.故|AB|≥2![]() ,当且仅当|OA|=|OB|=2时,等号成立.
,当且仅当|OA|=|OB|=2时,等号成立.
故|AB|的最小值为2![]() .
.
方法二:由(2)知|AB|2=3〔|AB|2=3(x12+x22)-4,3x12x22=4(x12+x22)-4〕.
设a=x12,b=x22,则a>0,b>0,ab≤(![]() )2,
)2,
4(a+b)-4≤3(![]() )2,a+b≥4或a+b≤
)2,a+b≥4或a+b≤![]() .
.
当a+b≤![]() 时,|AB|2≤0(不合,舍去);
时,|AB|2≤0(不合,舍去);
当a+b≥4时,|AB|2=3(a+b)-4≥8,|AB|≥2![]() ,当且仅当a=b=2,即x1=x2=±
,当且仅当a=b=2,即x1=x2=±![]() 时取等号.
时取等号.
故|AB|的最小值为2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| PF1 |
| PF2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| BF |
| ||
| 2 |
| a |
| b |
| a |
| b |
| a |
| b |
| 5 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| BF |
| ||
| 2 |
| a |
| b |
| a |
| b |
| a |
| b |
| 5 |
| 4 |
| A.1 个 | B.2 个 | C.3 个 | D.4 个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列四个命题:
① ![]() 是
是![]() 的充要条件;
的充要条件;
![]() ② 已知A、B是双曲
② 已知A、B是双曲![]() 线
线![]() 实轴的两个端点,M,N是双曲线上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且
实轴的两个端点,M,N是双曲线上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且![]() 的最小值为2,则双曲线的离心率e=
的最小值为2,则双曲线的离心率e=![]() ;
;
③ 取一根长度为3 m的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于1 m的概率是![]() ;
;
④ 一个圆形纸![]() 片,圆心为O,F为圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于P,则P的轨迹是椭圆。
片,圆心为O,F为圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于P,则P的轨迹是椭圆。
其中真命题的序号是 。(填上所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列四个命题:
① ![]() 是
是![]() 的充要条件;
的充要条件;
![]() ② 已知A、B是双曲
② 已知A、B是双曲![]() 线
线![]() 实轴的两个端点,M,N是双曲线上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且
实轴的两个端点,M,N是双曲线上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且![]() 的最小值为2,则双曲线的离心率e=
的最小值为2,则双曲线的离心率e=![]() ;
;
③ 取一根长度为3 m的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于1 m的概率是![]() ;
;
④ 一个圆形纸![]() 片,圆心为O,F为圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于P,则P的轨迹是椭圆。
片,圆心为O,F为圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于P,则P的轨迹是椭圆。
其中真命题的序号是 。(填上所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com