
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源: 题型:解答题
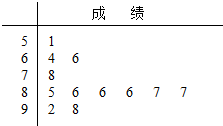 北京时间2015年07月31日17时57分,在马来西亚首都吉隆坡举行的国际奥委会第128次全会上,国际奥委会主席托马斯.巴赫宣布北京赢得2022年第二十四届冬季奥林匹克运动会(以下简称冬奥会)的举办权,华夏大地一片欢腾,某高中为了调查学生对冬奥会的了解惰况,组织了“冬奥会知多少”的知识问卷测试,从该校2400名学生中随机抽取12人进行知识问卷测试,测试成绩(百分制)以茎叶图形式表示(如图所示),根据主办方标准,测试成绩低于80分的为“非体育迷”,不低于80分的为“体育迷”,
北京时间2015年07月31日17时57分,在马来西亚首都吉隆坡举行的国际奥委会第128次全会上,国际奥委会主席托马斯.巴赫宣布北京赢得2022年第二十四届冬季奥林匹克运动会(以下简称冬奥会)的举办权,华夏大地一片欢腾,某高中为了调查学生对冬奥会的了解惰况,组织了“冬奥会知多少”的知识问卷测试,从该校2400名学生中随机抽取12人进行知识问卷测试,测试成绩(百分制)以茎叶图形式表示(如图所示),根据主办方标准,测试成绩低于80分的为“非体育迷”,不低于80分的为“体育迷”,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (2)(3) | C. | (1)(4) | D. | (2)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{9}{16}$x | B. | y=±$\frac{3}{4}$x | C. | y=±$\frac{16}{9}$x | D. | y=±$\frac{4}{3}$x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com