
设圆C满足:(1)截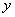 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被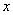 轴分成两段圆弧,其弧长的比为5∶1.
轴分成两段圆弧,其弧长的比为5∶1.
在满足条件(1)、(2)的所有圆中,求圆心到直线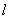 :3
:3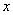 -4
-4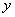 =0的距离最小的圆的方程.
=0的距离最小的圆的方程.
解:设所求圆的圆心为P(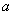 ,
,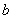 ),半径为
),半径为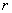 ,则P到
,则P到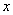 轴、
轴、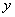 轴的距离分别为|
轴的距离分别为|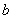 |、|
|、|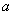 |.
|.
由题设圆P截x轴所得劣弧所对圆心角为60°……2分,圆P截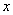 轴所得弦长为
轴所得弦长为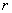 ,故 3
,故 3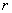 2=4
2=4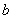 2,
2,
又圆P截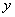 轴所得弦长为2,所以有r2=
轴所得弦长为2,所以有r2=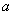 2+1,…………5分
2+1,…………5分
从而有4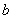
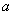 2=3
2=3
又点P(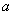 ,
,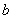 )到直线3
)到直线3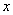 -4
-4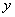 =0距离为
=0距离为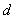 =
=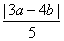 ,…………7分
,…………7分
所以25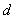 2=|3
2=|3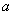 -4
-4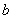 |2
|2
=9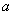 2+16
2+16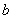
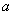
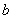 ≥9
≥9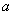 2+16
2+16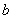 (
(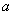 2+
2+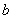 2)………10分
2)………10分
=4b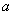 2=3
2=3
当且仅当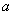 =
=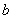 时上式等号成立,此时25
时上式等号成立,此时25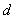 2=3,从而
2=3,从而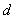 取得最小值,
取得最小值,
由此有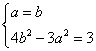 ,解方程得
,解方程得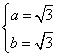 或
或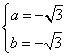 ………12分
………12分
由于3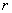 2=4
2=4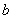 2,知
2,知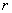 =2,于是所求圆的方程为
=2,于是所求圆的方程为
(x-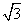 )2+(y-
)2+(y-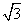 )2=4或(x+
)2=4或(x+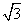 )2+(y+
)2+(y+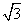 2=4……….13分
2=4……….13分


科目:高中数学 来源: 题型:
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.1 1 |
| 2 |
| π |
| 4 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| CM |
| CP |
| MF |
| MP |
| FR |
| FS |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (本小题满分14分)设b>0,椭圆方程为
(本小题满分14分)设b>0,椭圆方程为![]() ,抛物线方程为
,抛物线方程为![]() 。如图所示,过点F(0,b + 2)作x轴的平行线,与抛物线在第一象限的交点为G。已知抛物线在点G的切线经过椭圆的右焦点F1。
。如图所示,过点F(0,b + 2)作x轴的平行线,与抛物线在第一象限的交点为G。已知抛物线在点G的切线经过椭圆的右焦点F1。
(1)求满足条件的椭圆方程和抛物线方程;
(2)点G、![]() 所在的直线截椭圆的右下区域为D,
所在的直线截椭圆的右下区域为D,
若圆C:![]() 与区域D有公共点,求m的最小值。
与区域D有公共点,求m的最小值。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省高州市高三上学期16周抽考数学理卷 题型:解答题
(本小题满分13分)设圆C满足:(1)截 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被 轴分成两段圆弧,其弧长的比为5∶1.在满足条件(1).(2)的所有圆中,求圆心到直线
轴分成两段圆弧,其弧长的比为5∶1.在满足条件(1).(2)的所有圆中,求圆心到直线 :3
:3 -4
-4 =0的距离最小的圆的方程.
=0的距离最小的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com