
【题目】已知函数![]() .
.
(1)求![]() 的定义域和值域;
的定义域和值域;
(2)求![]() 的单调区间;
的单调区间;
(3)设![]() 的反函数为
的反函数为![]() ,解关于x的方程:
,解关于x的方程:![]() .
.
【答案】(1)见解析;(2)见解析;(3)当![]() 时,原方程的根为
时,原方程的根为![]() ;当
;当![]() 时,原方程的根为
时,原方程的根为![]() .
.
【解析】
(1)先根据真数大于零列不等式,再分![]() 和
和![]() 进行讨论解得定义域;最后在定义域下求真数范围,即得
进行讨论解得定义域;最后在定义域下求真数范围,即得![]() 的值域;
的值域;
(2)先确定原函数为指数函数与对数函数的复合,再在定义域下分![]() 和
和![]() 进行讨论
进行讨论![]() 的单调区间;
的单调区间;
(3)先求反函数得![]() ,再根据对数性质、指数性质解方程得
,再根据对数性质、指数性质解方程得![]() 或
或![]() ,最后验根.
,最后验根.
(1)当![]() 时,由
时,由![]() ,即
,即![]() 的定义域为
的定义域为![]() ;
;
又![]() 且
且![]() ,∴
,∴![]() ,即
,即![]() 的值域为
的值域为![]() .
.
同理,当![]() 时,
时,![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() .
.
(2)设![]() ,
,![]() 时,
时,![]() 是
是![]() 上的减函数,
上的减函数,![]() 是增函数,故
是增函数,故![]() 是
是![]() 上的减函数;当
上的减函数;当![]() 时,
时,![]() 是
是![]() 上的增函数,
上的增函数,![]() 是减函数,故
是减函数,故![]() 是
是![]() 上的减函数.
上的减函数.
(3)∵![]() ,∴
,∴![]() 等价于
等价于![]() .该方程可化为
.该方程可化为![]() .
.
解方程,得![]() 或
或![]() .
.
经检验:当![]() 时,原方程的根为
时,原方程的根为![]() ;当
;当![]() 时,原方程的根为
时,原方程的根为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为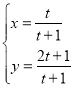 (t为参数),曲线C2的参数方程为
(t为参数),曲线C2的参数方程为![]() (α为参数),以坐标原点为极点.x轴正半轴为极轴建立极坐标系.
(α为参数),以坐标原点为极点.x轴正半轴为极轴建立极坐标系.
(Ⅰ)求曲线C1的普通方程和曲线C2的极坐标方程;
(Ⅱ)射线![]() 与曲线C2交于O,P两点,射线
与曲线C2交于O,P两点,射线![]() 与曲线C1交于点Q,若△OPQ的面积为1,求|OP|的值.
与曲线C1交于点Q,若△OPQ的面积为1,求|OP|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明每天从家步行去学校,有两条路线可以选择,第一条路线,需走天桥,不用等红灯,平均用时910秒;第二条路线,要经过两个红绿灯路口,如图,A处为小明家,D处为学校,走路段![]() 需240秒,在B处有一红绿灯,红灯时长120秒,绿灯时长30秒,走路段
需240秒,在B处有一红绿灯,红灯时长120秒,绿灯时长30秒,走路段![]() 需450秒,在C处也有一红绿灯,红灯时长100秒,绿灯时长50秒,走路段
需450秒,在C处也有一红绿灯,红灯时长100秒,绿灯时长50秒,走路段![]() 需200秒.小明进行了60天的试验,每天都选择第二条路线,并记录了在B处等待红灯的时长,经统计,60天中有48天在B处遇到红灯,根据记录的48天等待红灯时长的数据绘制了下面的频率分布直方图.已知B处和C处的红灯亮起的时刻恰好始终保持相同,且红绿灯之间切换无时间间隔.
需200秒.小明进行了60天的试验,每天都选择第二条路线,并记录了在B处等待红灯的时长,经统计,60天中有48天在B处遇到红灯,根据记录的48天等待红灯时长的数据绘制了下面的频率分布直方图.已知B处和C处的红灯亮起的时刻恰好始终保持相同,且红绿灯之间切换无时间间隔.

(1)若小明选择第二条路线,设当小明到达B处的时刻为B处红灯亮起后的第x秒(![]() )时,小明在B处等待红灯的时长为y秒,求y关于x的函数的解析式;
)时,小明在B处等待红灯的时长为y秒,求y关于x的函数的解析式;
(2)若小明选择第二条路线,请估计小明在B处遇到红灯的概率,并问小明是否可能在B处和C处都遇到红灯;
(3)若取区间中点作为该区间对应的等待红灯的时长,以这两条路线的平均用时作为决策依据,小明应选择哪一条路线?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图.则下列说法不正确的是( )

A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数
B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果,但防控要求不能降低
C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天
D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左、右焦点分别为F1、F2,过点F1作圆x2+y2=a2的切线交双曲线右支于点M,若tan∠F1MF2=2,又e为双曲线的离心率,则e2的值为( )
的左、右焦点分别为F1、F2,过点F1作圆x2+y2=a2的切线交双曲线右支于点M,若tan∠F1MF2=2,又e为双曲线的离心率,则e2的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图中有一个信号源和五个接收器.接收器与信号源在同一个串联线路中时,就能接收到信号,否则就不能接收到信号.若将图中左端的六个接线点随机地平均分成三组,将右端的六个接线点也随机地平均分成三组,再把所得六组中每组的两个接线点用导线连接,则这五个接收器能同时接收到信号的概率是( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是![]() ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(1)从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.求恰好摸5次停止的概率;
(2)若A,B两个袋子中的球数之比为![]() ,将A,B中的球装在一起后,从中摸出一个红球的概率是
,将A,B中的球装在一起后,从中摸出一个红球的概率是![]() ,求p的值.
,求p的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厂家在产品出厂前,需对产品做检验.厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(1)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验,求至少有1件是合格品的概率;
(2)若厂家发给商家20件产品,其中有3件不合格.按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家拒收这批产品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一排![]() 个空位,四人就坐其中的
个空位,四人就坐其中的![]() 个位子.
个位子.
(1)若每人左、右两边都有空位,有几种坐法?
(2)若![]() 个空位中,
个空位中,![]() 个相连,另
个相连,另![]() 个也相连,但
个也相连,但![]() 个不连在一起,有几种坐法?
个不连在一起,有几种坐法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com