练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (2006·北京)已知点M(－2，0)，N(2，0)，动点P满足条件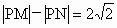，设动点P的轨迹为W．

    (1)求W的方程；

    (2)若A，B是W上的不同两点，O是坐标原点，求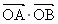的最小值．

    答案：略
    解析：

    解法一：

    (1)由知动点P的轨迹是以M，N为焦点的双曲线的右支，实半轴长．

    又半焦距c=2，故虚半轴长．

    所以W的方程为．

    (2)设A，B的坐标分别为，．

    当轴时，，从而，

    ．

    当AB不与x轴垂直时，设直线AB的方程为y=kx＋m，与W的方程联立，消去y得

    ．

    故，所以

    又因为，所以，从而．

    综上，当轴时，取得最小值2．

    解法二：

    (1)同解法一．

    (2)设A，B的坐标分别为，，，则

    ．令，，则，且．所以

    当且仅当，即时“=”成立．

    所以的最小值是2．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：013

    (2006北京东城模拟)已知直线y=2x上一点P的横坐标为a，有两个点A(－1，1)，B(3，3)，那么使向量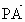与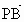夹角为钝角的一个充分但不必要的条件是

    [　　]

    A．－1＜a＜2

    B．0＜a＜1

    C．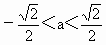

    D．0＜a＜2

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    (2006北京东城模拟)已知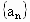是首项为1，公比为q的等比数列，．

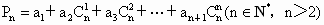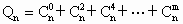
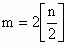    （其中，[t]表示不大于t的最大整数，例如[2.5]=2）．如果数列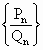有极限，那么公比q的取值范围是

    [　　]

    A．－1＜q≤1，且q≠0

    B．－1＜q＜1，且q≠0

    C．－3＜q≤1，且q≠0

    D．－3＜q＜1，且q≠0

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    (2006北京东城模拟)在△ABC中，已知sinC=2sin(B＋C)cosB，那么△ABC一定是

    [　　]

    A．等腰直角三角形

    B．等腰三角形

    C．直角三角形

    D．等边三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    (2006北京崇文模拟)已知，则的值为

    [　　]

    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    (2006北京东城模拟)一个电子元件，出厂前要进行五项指标检查，如果至少有两项指标不合格，则这个元件不能出厂，已知每项指标是否合格是相互独立的，且每项检查出现不合格的概率都是．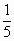

    (1)求这个电子元件不能出厂的概率；

    (2)某个这种元件直到五项指标全部检查完，才能确定该元件是否可以出厂，求这种情况的概率．

    查看答案和解析>>

    同步练习册答案