
| 1 |
| 2 |
| 5 |
| 4 |
| 19 |
| 32 |
| 19 |
| 32 |
| 1 |
| 2 |
| 5 |
| 4 |
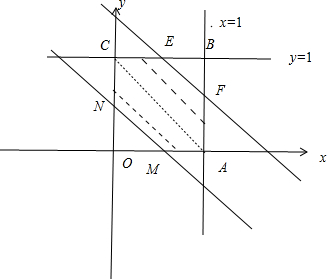 解:设所取的两个数分别为x,y,则
解:设所取的两个数分别为x,y,则
|
| 1 |
| 2 |
| 5 |
| 4 |
|
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 19 |
| 32 |
| 19 |
| 32 |
| 19 |
| 32 |


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源:陕西省模拟题 题型:解答题
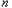 个,已知从袋子随机抽取1个小球,取到标号为2的小球的概率是
个,已知从袋子随机抽取1个小球,取到标号为2的小球的概率是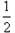 .
.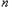 的值;
的值; 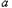 ,第二次取出的小球标号为
,第二次取出的小球标号为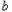 .
.  ”为事件A,求事件A的概率;
”为事件A,求事件A的概率; 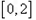 内任取2个实数
内任取2个实数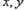 ,求事件“
,求事件“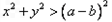 恒成立”的概率.
恒成立”的概率.查看答案和解析>>
科目:高中数学 来源: 题型:
下列四个命题:
①在区间![]() 内任取两个实数
内任取两个实数![]() ,则事件“
,则事件“![]() 恒成立”的概率是
恒成立”的概率是![]() ;
;
②函数![]() 关于(3,0)点对称,满足
关于(3,0)点对称,满足![]() ,且当
,且当![]() 时函
时函
数为增函数,则![]() 在
在![]() 上为减函数;
上为减函数;
③满足![]() ,
,![]() ,
,![]() 的
的![]() 有两解.
有两解.
其中正确命题的个数为
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
下列四个命题:
①在区间![]() 内任取两个实数
内任取两个实数![]() ,则事件“
,则事件“![]() 恒成立”的概率是
恒成立”的概率是![]() ;
;
②函数![]() 关于(3,0)点对称,满足
关于(3,0)点对称,满足![]() ,且当
,且当![]() 时函
时函
数为增函数,则![]() 在
在![]() 上为减函数;
上为减函数;
③满足![]() ,
,![]() ,
,![]() 的
的![]() 有两解.
有两解.
其中正确命题的个数为
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com