
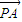 与
与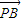 的夹角为钝角,则a的取值范围是 .
的夹角为钝角,则a的取值范围是 . 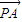 和
和 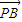 的坐标,由于向量
的坐标,由于向量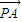 与
与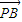 的夹角为钝角,则
的夹角为钝角,则 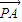 与
与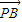 不平行,由此可得a的范围.再由
不平行,由此可得a的范围.再由 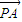 •
•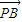 =5a(a-2)<0,可得a的范围.再把这两个a的范围取交集,即得所求.
=5a(a-2)<0,可得a的范围.再把这两个a的范围取交集,即得所求.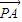 =(-1-a,1-2a),
=(-1-a,1-2a),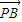 =(3-a,3-2a),
=(3-a,3-2a),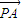 与
与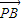 的夹角为钝角,则
的夹角为钝角,则 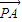 与
与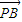 不平行,即 (-a-1)(3-2a)-(1-2a)(3-a)≠0,
不平行,即 (-a-1)(3-2a)-(1-2a)(3-a)≠0,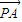 •
•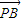 =(-a-1)(3-a)+(1-2a)(3-2a)=5a(a-2)<0,
=(-a-1)(3-a)+(1-2a)(3-2a)=5a(a-2)<0,

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
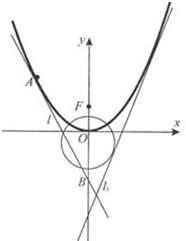 如图,已知直线
如图,已知直线| l | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省洛阳市高一(上)期末数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com