
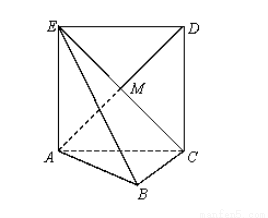
如图,正方形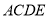 所在的平面与平面
所在的平面与平面 垂直,
垂直,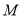 是
是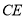 和
和 的交点,
的交点,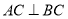 ,且
,且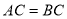 .
.
(1)求证: 平面
平面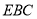 ;
;
(2)求二面角 的大小.
的大小.
(1)详见解析;(2) .
.
【解析】
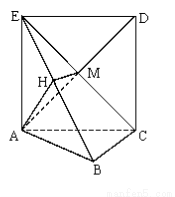
试题分析:(1)要证AM⊥平面EBC,关键是寻找线线垂直,利用四边形ACDE是正方形,可得AM⊥EC.利用平面ACDE⊥平面ABC,BC⊥AC,可得BC⊥平面EAC,从而有BC⊥AM.故可证;
(2)先求出二面角A-EB-C的平面角. 再在Rt△EAB中,利用AH⊥EB,有AE•AB=EB•AH.设EA=AC=BC=2a可得AB=2 a,EB=2
a,EB=2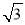 a,∴AH=
a,∴AH=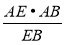 =
= .从而可求二面角A-EB-C的平面角 .
.从而可求二面角A-EB-C的平面角 .
证明:(1)∵四边形 是正方形,
是正方形,
∵平面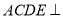 平面
平面 ,又∵
,又∵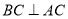 ,
,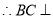 平面
平面 .
.
 平面
平面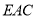 ,
,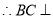
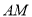 .
. 平面
平面 . 6分
. 6分
(2)过 作
作 于
于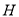 ,连结
,连结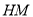 .
.
 平面
平面 ,
, .
. 平面
平面 .
.
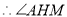 是二面角
是二面角 的平面角.
的平面角.
∵ 平面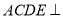 平面
平面 ,
, 平面
平面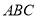 .
.

 .
.
在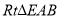 中,
中,  ,有
,有 .
.
设 可得
可得
 ,
, ,
,
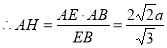 .
.  .
. 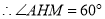 .
.
∴二面角 等于
等于 . 12分.
. 12分.
考点:1.用空间向量求直线与平面的夹角; 2.用空间向量求平面间的夹角.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015届河北省唐山市高三年级摸底考试文科数学试卷(解析版) 题型:解答题
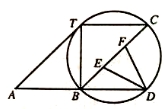
如图,⊙O过平行四边形ABCT的三个顶点B,C,T,且与AT相切,交AB的延长线于点D.
(1)求证:AT2=BT·AD;
(2)E、F是BC的三等分点,且DE=DF,求∠A.
查看答案和解析>>
科目:高中数学 来源:2015届河北省保定市高二下学期期中考试理科数学试卷(解析版) 题型:填空题
已知正三角形内切圆的半径 与它的高
与它的高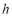 的关系是:
的关系是: ,把这个结论推广到空间正四面体,则正四面体内切球的半径
,把这个结论推广到空间正四面体,则正四面体内切球的半径 与正四面体高
与正四面体高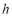 的关系是 .
的关系是 .
查看答案和解析>>
科目:高中数学 来源:2015届河北省“五个一名校联盟”高三教学质量监测一文科数学试卷(解析版) 题型:解答题
在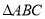 中,角
中,角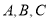 所对的边分别是
所对的边分别是 ,已知
,已知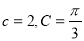 .
.
(1)若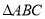 的面积等于
的面积等于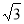 ,求
,求 ;
;
(2)若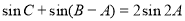 ,
,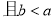 ,求
,求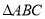 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com