
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
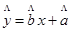
科目:高中数学 来源:不详 题型:解答题
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
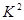
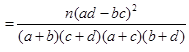 (
( )
)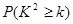 | 0.050 | 0.010 | 0.001 |
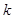 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
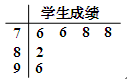
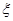 为这两位同学中成绩低于平均分的人数,求
为这两位同学中成绩低于平均分的人数,求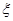 的分布列和期望.
的分布列和期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
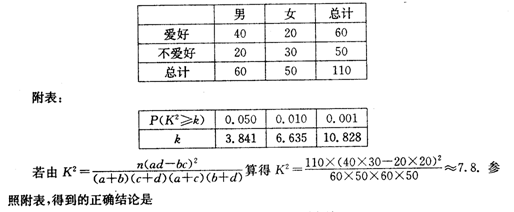
| A.有99%以上的把握认为“爱好该项运动与性别有关” |
| B.有99%以上的把握认为“爱好该项运动与性别无关” |
| C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” |
| D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(min) | 62 | m | n | 81 | 89 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在 的学生人数为6.
的学生人数为6. 和
和 这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在 恰有1人的概率.
恰有1人的概率.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
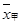 、
、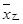 表示,则下列结论正确的是( )
表示,则下列结论正确的是( )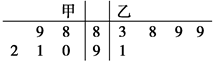
A.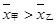 ,且甲比乙成绩稳定 ,且甲比乙成绩稳定 | B.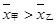 ,且乙比甲成绩稳定 ,且乙比甲成绩稳定 |
C.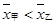 ,且甲比乙成绩稳定 ,且甲比乙成绩稳定 | D.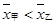 ,且乙比甲成绩稳定 ,且乙比甲成绩稳定 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示. 
 的值
的值查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 位工人某天生产该产品的数量,产品数量的分组区间为
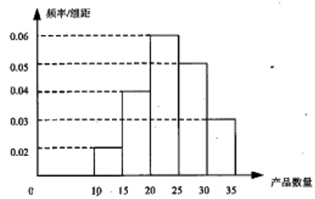
位工人某天生产该产品的数量,产品数量的分组区间为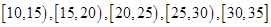 ,得到如题(16)图所示的频率分布直方图。已知生产的产品数量在
,得到如题(16)图所示的频率分布直方图。已知生产的产品数量在 之间的工人有6位.
之间的工人有6位. ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com