
(文)数列{an}中a1=0,![]() ,(1)求证数列
,(1)求证数列![]() 为等差数列,并求出公差;(2)设数列{an}的前n项和为Sn,证明Sn<n-ln(n+1);(3)设
为等差数列,并求出公差;(2)设数列{an}的前n项和为Sn,证明Sn<n-ln(n+1);(3)设![]() ,证明:对任意正整数n,m,都有
,证明:对任意正整数n,m,都有![]() .
.
(1)略 (2)略
(1)∵![]() 即
即![]() ,∴公差d=-1.
,∴公差d=-1.
且首项为![]() ,故
,故![]() 是等差数列.
是等差数列.
(2)∵![]() ,∴
,∴![]() .
.
设f(x)=x-ln(x+1),(x>0),则![]() ,f(x)在(0,+∞)↑,且f(x)在[0,+∞)上连续,∴f(x)>f(0)=0,∴x>0时x>ln(x+1), ∴
,f(x)在(0,+∞)↑,且f(x)在[0,+∞)上连续,∴f(x)>f(0)=0,∴x>0时x>ln(x+1), ∴![]() ,即
,即![]() .
.
∴an<1-ln(n+1)+lnn,∴Sn<(1-ln2+ln1)+(1-ln3+ln2)+…+[1-ln(n+1)+lnn]=n-ln(n+1)故Sn<n-ln(n+1).
(3)∵![]() ,∴
,∴![]() ,当
,当![]() 时,则
时,则![]() ,∴
,∴![]() ,
,
即n≥4;又当![]() 时,则
时,则![]() ,即n≤3,因此得b1<b2<b3<b4>b5>b6>…,又∵b1=0,n≥2时,bn>0,∴0≤bn≤b4.∴对任意正整数n、m,都有
,即n≤3,因此得b1<b2<b3<b4>b5>b6>…,又∵b1=0,n≥2时,bn>0,∴0≤bn≤b4.∴对任意正整数n、m,都有![]()


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
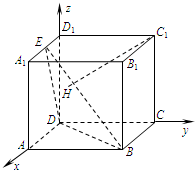 [理]如图,在正方体ABCD-A1B1C1D1中,E是棱A1D1的中点,H为平面EDB内一点,
[理]如图,在正方体ABCD-A1B1C1D1中,E是棱A1D1的中点,H为平面EDB内一点,| HC1 |
| 1 |
| (n+1)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a1 |
| 2k1-1 |
| a2 |
| 2k2-1 |
| an |
| 2kn-1 |
查看答案和解析>>
科目:高中数学 来源:山东省郓城一中2012届高三上学期寒假作业数学试卷(13) 题型:044
(文)在数列{an}中,a1=1,an+1=an+c(c为常数,n∈N*),且a1,a2,a5成公比不等于1的等比数列.
(Ⅰ)求c的值;
(Ⅱ)设![]() ,求数列{bn}的前n项和Sn
,求数列{bn}的前n项和Sn
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com